Chapter 8 - Causal Paths and Closing Back Doors
8.1 I Walk the Line
Previous chapters have emphasized the concept of the causal diagram. I, the author of this book, clearly have a thing for nodes and arrows.
The reason these diagrams can be so useful for applied researchers is that they make clear the different reasons why two variables might be related to each other, and also what we need to do to identify the answer to our research question.
Both of these benefits of causal diagrams come about by thinking carefully about the paths from one variable to another on a diagram.
These paths tell us why - why are two variables related? Which causes the other? That’s the kind of crucial context we need to figure out our research question.
Those paths are what this chapter is all about.
Path. A path on a causal diagram is the set of arrows and nodes you pass when going from one variable to another.
What is a path? A path between two variables on a causal diagram is a description of the set of arrows and nodes you visit when “walking” from one variable to another.
For example, consider the below diagram Figure 8.1. We can observe in data that B and C are related. But why are they related?
Figure 8.1: An Example Causal Diagram for Path-Finding

One reason is that B causes C. After all, B \(\rightarrow\) C is on the diagram - that’s one path between B and C.
Another reason is that D causes both E and C, and E causes B. In other words, we have the path B \(\leftarrow\) E \(\leftarrow\) D \(\rightarrow\) C. We can “walk” from B to E, and then onwards to D, and finally to C. We’ve taken a nice little stroll along the paths laid out on our diagram, and moved from one variable, B, to another, C.121 There’s a third way to go, too: B \(\leftarrow\) A \(\leftarrow\) E \(\leftarrow\) D \(\rightarrow\) C.
So why are B and C related? As mentioned, one reason is that B causes C. The path B \(\rightarrow\) C is on the diagram. Another is that D causes C, and D also causes E, which causes B. In other words, B and C appear to move together because they’re both caused by D.
If our research question is about the effect of B on C, then this second pathway - the one that D is responsible for, is another reason we would see B and C being related other than B \(\rightarrow\) C. It’s an alternate explanation for why B and C might be related, other than the explanation that answers our research question of whether (and how much) B causes C.
The paths can tell us the road we want to walk on, and also the road we want to avoid. They’re crucial for figuring out our identification. So let’s learn about them.
8.2 Any Way You Like It
Our first task will be finding all the paths. That’s right, all of them. We want to be able to write out every single path that starts with the treatment variable and ends with the outcome variable.
Why do we need to be sure to get every path? Because each path explains one way in which the treatment and outcome variables might be related. They’re alternate explanations. For example, if we are looking at the effect of smoking on cancer, and one path is Smoking \(\rightarrow\) Cancer, and another is Smoking \(\leftarrow\) Income \(\rightarrow\) Cancer, then if you say “smoking causes cancer,” then someone else could, quite reasonably, say “maybe, but also, being low-income can affect both whether you smoke and your health generally, so maybe it’s just a statistical illusion!”
If you want to really show how much your treatment causes your outcome, you have to be able to find those alternate explanations so you can account for them in your research and identify just the explanation you’re interested in.
Those alternate explanations live on the paths. If we want to destroy them, first we must know them.
So how can we find every path from treatment to outcome?122 This method also works for finding paths between two variables that aren’t treatment and outcome, which comes in handy in some cases, including later in this chapter when we test the diagram. There might be lots of paths on a more complex graph. So how can we find them?
We can follow a few convenient steps:
- Start at the treatment variable
- Follow one of the arrows coming in or out (either is fine!) of the treatment variable to find another variable
- Then, follow one of the arrows coming in or out of that variable
- Keep repeating step 3 until you either come to a variable you’ve already visited (a loop! That’s not a path), or find the outcome variable (that’s a path. Write it down)
- Every time you either find a path or a loop, back up one and try a different arrow in/out until you’ve tried them all. Then, back up again and try all those arrows
- Once you’ve tried all the ways out of the treatment variable and all the eventual paths, you’ve got all the paths!
Let’s do a quick example with a simple diagram in Figure 8.2.
Figure 8.2: Diagram on Which We Will Look for Paths
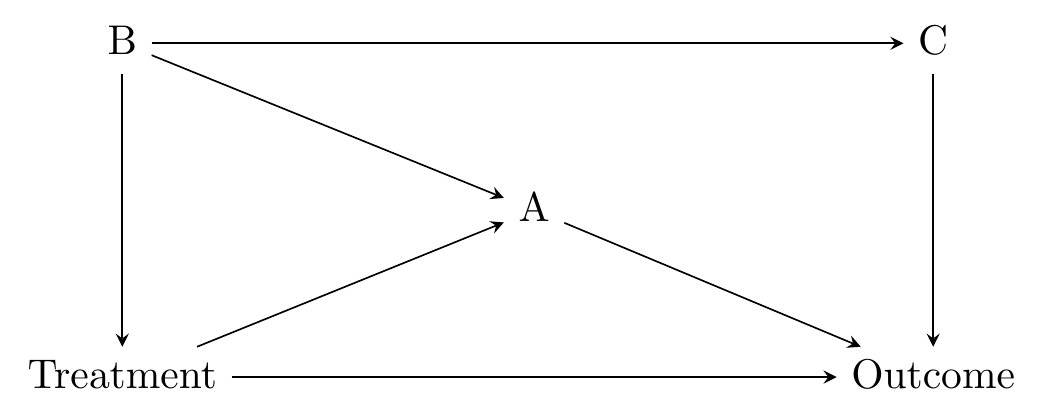
Let’s follow the steps outlined above.123 If this seems tedious (and it is), don’t worry. Once you’ve done this to a few diagrams, you’ll start to be able to spot all the paths without having to go through this slog.
- Start at Treatment.
- Let’s follow an arrow. Let’s go straight to Outcome.
- We’ve reached Outcome, so that’s a path. Treatment \(\rightarrow\) Outcome is a path.
- Back up to Treatment. Follow another arrow. This time to A.
- Now follow an arrow out of A. Let’s go to Outcome. Done! Treatment \(\rightarrow\) A \(\rightarrow\) Outcome is a path.
- Back up to A. Take the other arrow out to B.
- Where can we go from here? Only to C without repeating a variable.
- And from C we can only go to Outcome. Done! Treatment \(\rightarrow\) A \(\leftarrow\) B \(\rightarrow\) C \(\rightarrow\) Outcome is a path.
- Back up to B, but there’s nowhere else to go.
- Back up to A, and there’s nowhere else to go.
- Back up to Treatment. The only arrow left is B.
- From B we can go to A, and then on to Outcome. Done! Treatment \(\leftarrow\) B \(\rightarrow\) A \(\rightarrow\) Outcome is a path.
- Back up to A, then back up to B. Only path remaining is C, then Outcome. Done! Treatment \(\leftarrow\) B \(\rightarrow\) C \(\rightarrow\) Outcome is a path.
- Back up to C, nowhere to go, back up to B, nowhere else to go, back up to Treatment, nowhere else to go. We’ve exhausted all the possibilities. We’re done!
The full list of paths is:
- Treatment \(\rightarrow\) Outcome
- Treatment \(\rightarrow\) A \(\rightarrow\) Outcome
- Treatment \(\rightarrow\) A \(\leftarrow\) B \(\rightarrow\) C \(\rightarrow\) Outcome
- Treatment \(\leftarrow\) B \(\rightarrow\) A \(\rightarrow\) Outcome
- Treatment \(\leftarrow\) B \(\rightarrow\) C \(\rightarrow\) Outcome
Let’s practice. The example diagram in Figure 8.3 has a few more moving parts so we can try to work through the full list of paths. Give it a shot yourself first - try to find all the paths you can, and then see how well you’ve matched up to the full list.
Figure 8.3 shows the relationship between drinking wine and your lifespan. There are a few reasons why you might expect people who drink more wine to live longer. Perhaps wine itself really does have a causal effect on your lifespan, for one. Also, the kinds of people who choose to drink wine might also live longer for other reasons, such as their baseline level of health or their income.124 “Health” here is meant to imply a baseline level of health, i.e., how healthy you might be before drinking (or not drinking) wine. Also, maybe wine drinking affects your penchant for taking other drugs (perhaps as a substitute?) and so affects your lifespan in that way. All of that is on the diagram.
Figure 8.3: The Effect of Wine on Lifespan
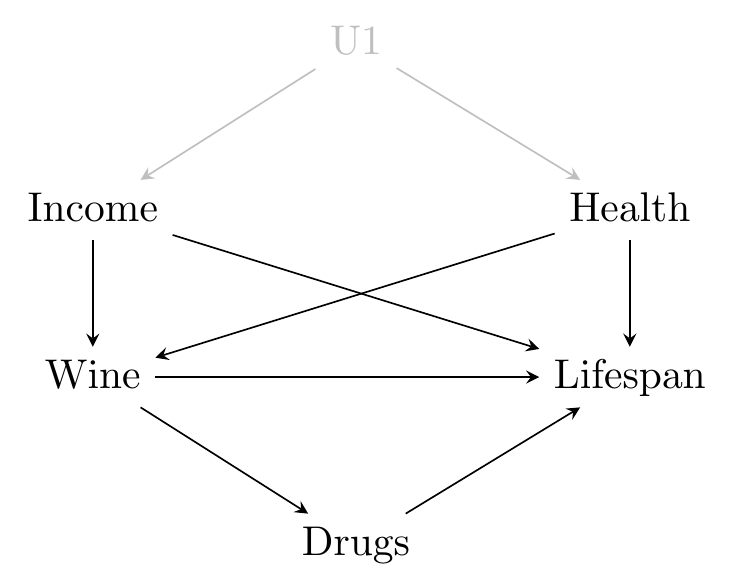
Let’s follow our steps and see where it leads us.
- From Wine, we can go to Lifespan. Easy. Wine \(\rightarrow\) Lifespan.
- Now back to Wine. The next arrow out is Drugs, which only goes to Lifespan. Wine \(\rightarrow\) Drugs \(\rightarrow\) Lifespan.
- Back to Drugs, no other way out, so back to Wine. Next out let’s go to Income.
- From Income we can go to Lifespan: Wine \(\leftarrow\) Income \(\rightarrow\) Lifespan.
- Now back to Income. The only way out we haven’t covered is U1. From there we have to go to Health. And from Health, the only options are Wine and Lifespan. We’ve already visited Wine so the only way is Lifespan. Wine \(\leftarrow\) Income \(\leftarrow\) U1 \(\rightarrow\) Health \(\rightarrow\) Lifespan.
- Back to Health, every other arrow out is somewhere we’ve been. Then back to U1, then we have to go back to Income, and again we’ve already taken every arrow out already, so back to Wine.
- The only arrow we haven’t been out of yet is Health. So we go to Health and can then go on to Lifespan. Wine \(\leftarrow\) Health \(\rightarrow\) Lifespan.
- Back to Health. We can take the arrow to U1 out of Health, which goes to Income, which goes to Lifespan. Wine \(\leftarrow\) Health \(\leftarrow\) U1 \(\rightarrow\) Income \(\rightarrow\) Lifespan.
And there we have it. We’ve exhausted all the possible ways we can get from Wine to Lifespan. The full list of paths is:
- Wine \(\rightarrow\) Lifespan
- Wine \(\rightarrow\) Drugs \(\rightarrow\) Lifespan
- Wine \(\leftarrow\) Income \(\rightarrow\) Lifespan
- Wine \(\leftarrow\) Income \(\leftarrow\) U1 \(\rightarrow\) Health \(\rightarrow\) Lifespan
- Wine \(\leftarrow\) Health \(\rightarrow\) Lifespan
- Wine \(\leftarrow\) Health \(\leftarrow\) U1 \(\rightarrow\) Income \(\rightarrow\) Lifespan
And each of those paths contains a story - a reason why we’d see a relationship between Wine and Lifespan in data. Wine can affect your drug-taking, which affects your lifespan (Wine \(\rightarrow\) Drugs \(\rightarrow\) Lifespan). Or people who drink wine tend to be richer, and richer people live longer (Wine \(\leftarrow\) Income \(\rightarrow\) Lifespan). Or people who drink Wine tend to be richer, richer people on average have better health, and health improves your lifespan (Wine \(\leftarrow\) Income \(\leftarrow\) U1 \(\rightarrow\) Health \(\rightarrow\) Lifespan). A story for every path. But which stories matter to us?
8.3 Good Paths and Bad Paths, Front Doors and Back Doors
Now that we have our list of paths, what can we do with them?
The promise I’ve given you is that we can use these paths to figure out how to answer your research question. And we can. At this point, the next step in using the paths we’ve come up with is to figure out just exactly how they relate to your research question.
This brings us to the concept of Good Paths and Bad Paths.125 In this chapter, I’ll capitalize these terms to draw attention to them. That seems like it would get old real fast though, so I’ll limit that practice to just this chapter.
Good path. A causal path is good if it is describing a reason why treatment and outcome are related that answers your research question.
Bad path. A causal path is Bad if it is describing a reason why treatment and outcome are related that is unrelated to your research question, or is an alternate explanation of the data.
In short, Good Paths are the reasons why the treatment and outcome variables are related that you think should “count” for your research question. Bad paths are the paths that shouldn’t count, in other words the alternate explanations.
Front door path. A causal path where all the arrows point away from Treatment.
Back door path. A causal path where at least one arrow, somewhere along the line, is pointing back left towards the treatment variable.
Usually, this is as simple as “every path in which all the arrows face away from Treatment are Good Paths, and the rest are Bad Paths.” Paths where all the arrows face away from Treatment are also known as front door paths. The rest would then be “back door paths.” Paths with at least one arrow pointing towards Treatment are back door paths. So, usually, all the front door paths are good, and all the back door paths are bad.126 In Abel and Annie’s case in Chapter 5, the Good, front door path was through the basement window, and all the other Bad Paths out of the house were back door paths.
Taking Figure 8.3 as an example, there are two paths where all the arrows are going away from Wine: Wine \(\rightarrow\) Lifespan and Wine \(\rightarrow\) Drugs \(\rightarrow\) Lifespan. These are all the ways in which a change in Wine would cause a change in Lifespan. So these are our front door paths. And if our research question is “does Wine cause Lifespan?” then these front door paths are the Good Paths, and the other, back door paths are bad ones.
It might not be quite as simple as that depending on what your research question is. For example, if instead of asking “does Wine cause Lifespan?” you want to know “other than how it might affect drug-taking, does Wine cause Lifespan?”
With this research question, the Wine \(\rightarrow\) Drugs \(\rightarrow\) Lifespan suddenly becomes a path we’re not interested in, even though it’s a front door. If we look at the raw data, one reason why Wine and Lifespan would be related is because of Drugs. But we are no longer interested in that part of the effect! We might at this point consider it a Bad Path.
Direct effect. The causal path Treatment \(\rightarrow\) Outcome.
Research questions like this, where the only Good Path is Treatment \(\rightarrow\) Outcome, are looking for “direct effects.” They are uninterested in “indirect effects” that take detours through variables like Drugs.
So we have all our paths, and we’ve figured out which of them are Good and which are Bad. The key to identifying the answer to our research question, then, is to find a way to dig just the Good Paths out of the data without getting distracted by the Bad ones.
8.4 Open and Closed Paths
Those pesky Bad Paths can cause us some real trouble. But only as long as they’re open for business. Open for… trouble business. In the business for trouble? Troubling business. Put something cool here.
The presence of a path on your diagram means that there is a relationship between the variables at the beginning and end of the path explained by the variables along the path. Wine \(\rightarrow\) Drugs \(\rightarrow\) Lifespan means that Wine and Lifespan will be related partly because of how Wine affects Drugs. Wine \(\leftarrow\) Income \(\rightarrow\) Lifespan means that Wine and Lifespan will be related partly because of how Income affects both Wine and Lifespan.
Open path. A causal path is Open if all of the variables along the path have variation in the data.
Closed path. A causal path is Closed if at least one of the variables along the path has no variation in the data.
However, this is only true if the path is Open. A path is Open if all of the variables along that paths are allowed to vary. It is instead Closed if at least one of the variables along that path has no variation.
What do I mean by this? Let’s take Wine \(\rightarrow\) Drugs \(\rightarrow\) Lifespan as an example. If in our data set we have wine drinkers and non-wine drinkers, drug-users and non-drug users, and people with shorter and longer lifespans, then all the variables along this path have variation. They vary in value.
But what if we pick a data set in which nobody uses drugs? In this case, there’s no variation in Drugs, and thus none of the relationship between Wine and Lifespan can possibly be driven by Drugs. The path has Closed.127 You can also imagine also picking a sample in which nobody drinks wine - all the paths with Wine (i.e., all the paths) would Close. We obviously wouldn’t be able to study the effects of wine in that sample, since there aren’t any wine drinkers to compare the non-wine-drinkers too. Another way to say that is that all the paths are Closed.
That’s the basic idea - paths become Closed, and thus no longer a threat to our identification - if we can remove all the variation due to a variable along that path. Picking a sample in which there’s no variation in that variable, as we did by picking a sample where nobody did drugs, is one way to do that, although it’s not a particularly great way. There are other ways.
For now, let’s just assume we have some way of controlling for a variable. In other words, we have some way of statistically adjusting our data so as to remove all the variation in a variable and thus closing a path with that variable on it. Holding that variable constant and un-varying, if you prefer. We talked about how to do this by estimating conditional conditional means in Chapter 4.128 Or adding it as a control variable to a regression, as will be discussed further in Chapter 13. But this is a specific application of “controlling” - we’re speaking generally here. We could also do this, as just mentioned, by picking a data set where the variable doesn’t vary. Or by picking a set of untreated observations with very similar (or exactly the same) values of that variable.129 This last approach is called matching, and we will cover it much more thoroughly in Chapter 14.
If we can control for at least one variable on each of our Bad Paths without controlling for anything on one of our Good Paths, we have identified the answer to our research question.
And there it is. That’s how you do it.
Let’s try this out on our Wine study. As a recap, here’s the diagram again in Figure 8.4, as well as our list of paths:
Figure 8.4: The Effect of Wine on Lifespan
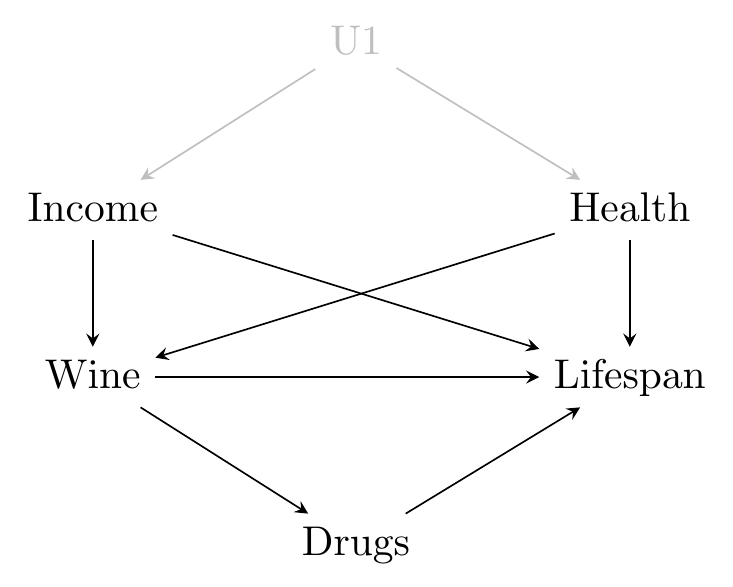
- *Wine \(\rightarrow\) Lifespan
- *Wine \(\rightarrow\) Drugs \(\rightarrow\) Lifespan
- Wine \(\leftarrow\) Income \(\rightarrow\) Lifespan
- Wine \(\leftarrow\) Income \(\leftarrow\) U1 \(\rightarrow\) Health \(\rightarrow\) Lifespan
- Wine \(\leftarrow\) Health \(\rightarrow\) Lifespan
- Wine \(\leftarrow\) Health \(\leftarrow\) U1 \(\rightarrow\) Income \(\rightarrow\) Lifespan
If we’re interested in the effect of Wine on Lifespan, we want all the ways in which Wine can cause Lifespan to change. We want all the Front Door Paths. We have two Front Door Paths, which are our Good Paths, marked with *. The rest are Bad Paths.
We can identify the answer to this research question by picking at least one variable along each Bad Path to control, without controlling for anything on a Good Path.
Let’s start by controlling for Income. What does that get us? Let’s turn all the Closed Paths gray to see. Income shows up in paths 3, 4, and 6, so those are all now Closed.
- *Wine \(\rightarrow\) Lifespan
- *Wine \(\rightarrow\) Drugs \(\rightarrow\) Lifespan
- Wine \(\leftarrow\) Income \(\rightarrow\) Lifespan
- Wine \(\leftarrow\) Income \(\leftarrow\) U1 \(\rightarrow\) Health \(\rightarrow\) Lifespan
- Wine \(\leftarrow\) Health \(\rightarrow\) Lifespan
- Wine \(\leftarrow\) Health \(\leftarrow\) U1 \(\rightarrow\) Income \(\rightarrow\) Lifespan</span
Only one Bad Path to close! If we control for Health we can do it. Controlling for both Health and Income we get…
- *Wine \(\rightarrow\) Lifespan
- *Wine \(\rightarrow\) Drugs \(\rightarrow\) Lifespan
- Wine \(\leftarrow\) Income \(\rightarrow\) Lifespan
- Wine \(\leftarrow\) Income \(\leftarrow\) U1 \(\rightarrow\) Health \(\rightarrow\) Lifespan
- Wine \(\leftarrow\) Health \(\rightarrow\) Lifespan
- Wine \(\leftarrow\) Health \(\leftarrow\) U1 \(\rightarrow\) Income \(\rightarrow\) Lifespan
So if we control for both Health and Income, any remaining relationship between Wine and Lifespan identifies the answer to our research question - what is the effect of Wine on Lifespan?130 Assuming our model was correct.
8.5 Colliders
There’s a wrinkle: Colliders. There’s something I’ve been leaving out about this whole Open and Closed Paths thing. So far, I’ve said that paths are Open as long as every variable along the path is allowed to vary, but removing the variation from a variable on the path (controlling/adjusting for it) Closes the path.
But that’s not always true. Specifically, that’s not true when there is a collider on the path. A variable is a collider on a particular path if, on that path, both arrows point at it.
Collider. A variable is a collider on a path if the arrows on either side of it both point at it.
For example, on the path Treatment \(\leftarrow\) A \(\rightarrow\) B \(\leftarrow\) C \(\rightarrow\) Outcome, B is a collider, since the arrows on either side of it on the path point towards it.131 A common mistake is to think that being a collider is a property of the variable - that some variables are colliders and others aren’t. Nope! Being a collider is a property of the variable on a particular pathway. The same variable might be a collider on one pathway and not a collider on another pathway. For example, if you look back at Figure 8.2, A is a collider on the Treatment \(\rightarrow\) A \(\leftarrow\) B \(\rightarrow\) C \(\rightarrow\) Outcome pathway, but not a collider on Treatment \(\rightarrow\) A \(\rightarrow\) Outcome. So if you don’t control for A, the first path is closed and the second is open, but if you do control for A, the first path is open and the second is closed (unless you also control for B or C).
When there’s a collider on the path, that path is Closed by default. That is, it’s Closed even if all of the variables on the path are allowed to vary.
Further, if you control for the collider, the path Opens back up! Thankfully, you can Close it back down again by controlling for another variable along the path.
Why does this happen? Why does it matter that both arrows are pointing at the variable?
You can think of it this way: the collider variable doesn’t cause anything else on the path. It’s just being caused by the variables to its left and right on the path. So if we’re looking for alternate explanations of why Treatment and Outcome might be related, the collider doesn’t actually give us one. It can’t drive a relationship along that path because it doesn’t drive anything on that path. It’s the thing being driven!
If the path were Treatment \(\leftarrow\) C \(\rightarrow\) Outcome, without a collider, then one reason why Treatment and Outcome vary together is because C causes them both. But with a collider, Treatment \(\leftarrow\) A \(\rightarrow\) B \(\leftarrow\) C \(\rightarrow\) Outcome, C can affect Outcome, and C can affect B, but because B doesn’t affect Treatment, C can no longer induce a relationship between Treatment and Outcome. B saved us.
Okay, so that’s why a collider Closes a path by default. But why does controlling for the collider Open it back up? Because once you control for the collider, the two variables pointing to the collider become related,132 Uh, why is that? For example, imagine your boss has a habit of ordering sandwiches for the whole office, but they always announce it after you’ve already ordered lunch. So we have the path Buy a Sandwich \(\rightarrow\) Eat a Sandwich \(\leftarrow\) Gifted A Sandwich. Whether you’ve bought a sandwich is totally unrelated to whether your boss gives you one. But if we know you Eat a Sandwich (i.e., control for the collider), they are related - if you didn’t Buy a Sandwich then you must have been Gifted A Sandwich. So now there’s a link from Buy a Sandwich and Gifted A Sandwich, and an alternate explanation can occur. and suddenly C can affect A and thus affect Treatment again. The alternate explanation returns.
Colliders seem like not a big deal. They’re only a problem if you control for them. So don’t control for them, right? Easy. Two problems with that. First, we need to figure out that a variable is a collider so we know not to control for it—if you aren’t careful, colliders are often disguised as variables it feels like you should control for—after all, they do belong on the diagram, so it seems reasonable to include it as a control, right? Second, one common way we control for colliders is by selecting a sample. Remember, picking a sample with no variation in \(Z\) is one way of controlling for \(Z\). So if you do a study, say, of college students, then you’re controlling for college attendance whether you want to or not. If college attendance is a collider on a Bad Path… oops!
What’s the goal, then? If we want to identify the answer to our research question, what we have to do is Close all the Bad Paths while leaving all the Good Paths Open. Once we’ve done that, any remaining relationship between Treatment and Control can only be going through the Good Paths, and all of the Good Paths we want are included. This is exactly what we want.
This takes a careful consideration of the diagram and the paths along it. Which ones are Good? Which are Bad? Which are Closed by default because of colliders? Which are Open and need one of the variables along it controlled for so it can be Closed? Can we be careful not to Close any Good Paths?
This is the process of identification.
8.6 Using Paths to Test Your Diagram
Before we move on, there’s one more neat trick we can play with causal paths.
Everything we’ve talked about so far has been about looking for paths between Treatment and Outcome. But that’s not all you can do in a diagram. We can look for paths between any two variables.
Now, this might not directly help us answer our research question, which really only cares about paths between Treatment and Outcome. But what it can do is help us determine whether we have the right diagram in the first place.
Let’s pick two variables on our diagram other than Treatment and Outcome. Let’s call them A and B. The basic idea is this: list all of the paths between A and B. Then, do what you need to do to make sure they’re all Closed.133 In the lingo of causal diagrams this is known as “d-separation.” The two variables are separated from each other by the control variables we’ve chosen. Then, if A and B are still related to each other (as might be determined using any of the methods in Chapter 4), that means there must be some other path you didn’t account for. Your diagram is deficient, and perhaps in an important way.
Let’s do a quick example, once again turning to wine. Let’s pick two variables on Figure 8.4. Let’s try it with Income and Drugs. What are all the paths between Drugs and Income? Using our steps from before, we get:
- Drugs \(\leftarrow\) Wine \(\leftarrow\) Income
- Drugs \(\leftarrow\) Wine \(\leftarrow\) Health \(\leftarrow\) U1 \(\rightarrow\) Income
- Drugs \(\leftarrow\) Wine \(\leftarrow\) Health \(\rightarrow\) Lifespan \(\leftarrow\) Income
- Drugs \(\leftarrow\) Wine \(\rightarrow\) Lifespan \(\leftarrow\) Income
- Drugs \(\leftarrow\) Wine \(\rightarrow\) Lifespan \(\leftarrow\) Health \(\leftarrow\) U1 \(\rightarrow\) Income
- Drugs \(\rightarrow\) Lifespan \(\leftarrow\) Income
- Drugs \(\rightarrow\) Lifespan \(\leftarrow\) Wine \(\leftarrow\) Income
- Drugs \(\rightarrow\) Lifespan \(\leftarrow\) Wine \(\leftarrow\) Health \(\leftarrow\) U1 \(\rightarrow\) Income
- Drugs \(\rightarrow\) Lifespan \(\leftarrow\) Health \(\rightarrow\) Wine \(\leftarrow\) Income
- Drugs \(\rightarrow\) Lifespan \(\leftarrow\) Health \(\leftarrow\) U1 \(\rightarrow\) Income
That’s a lot! But the list of Open Paths is much smaller, since Lifespan is a collider everywhere it turns up. The list of Open Paths is only:
- Drugs \(\leftarrow\) Wine \(\leftarrow\) Income
- Drugs \(\leftarrow\) Wine \(\leftarrow\) Health \(\leftarrow\) U1 \(\rightarrow\) Income
If we can then control for Wine, both of these paths Close too. What we’ve learned is that our diagram effectively makes the claim that there’s no way that Income and Drugs are related to each other except through the amount of wine you drink. That seems… unlikely. We can then check in the data to see if Income and Drugs are related after controlling for Wine. If they are (and they likely will be), our model is incomplete.
Tests like these, where we expect that a relationship should be zero because our diagram says there are no Open Paths, and we see whether it’s actually zero, are called placebo tests.134 In some fields like epidemiology, they call these “falsification tests” instead. They get the name because, like a placebo drug, there shouldn’t be anything there. But maybe there is anyway! We’ll be seeing plenty of placebo tests throughout this book.
Placebo test. Finding a relationship that your causal diagram says should be zero, and checking whether it’s actually zero.
Failing a placebo test is not the end of the world, thankfully. Yes, failing one of these tests does prove that your model is incorrect and incomplete. But let’s be honest, we already knew that before we started. Models necessarily leave things out. The question isn’t whether you’ve omitted anything, it’s how important the omission is.
So then what’s the point of these tests?
Well, even though failing a test doesn’t mean the end of the world, it should at least lead you to reflect on whether the model can be improved. Even the process of setting up the test can be informative. Did you notice when looking at the original Figure 8.4 that it implied that Income only affected Drugs through Wine? Maybe, or maybe not. Regardless, the test definitely made that clear.
Also, even if we find a relationship, there are degrees of relationship. If you find a small but nonzero relationship that, according to the diagram, shouldn’t be there, that might be a minor cause for concern. But if there’s an enormous and super-strong relationship that shouldn’t be there, that’s when you should really worry and maybe go back to the drawing board on your diagram.
8.7 Path Glossary
We’ve talked about a lot of different kinds of paths. Here are some reminders as to what these terms mean.
Good Path. A path that relates to your research question/a path you are trying to identify.
Bad Path. A path that is not related to your research question.
Front Door Path. A path where all the arrows point away from Treatment.
Back Door Path. A path where at least one of the arrows points towards Treatment.
Open Path. A path in which there is variation in all variables along the path (and no variation in any colliders on that path).
Closed Path. A path in which there is at least one variable with no variation (or a collider with variation).
Collider. A variable is a collider along a path if both arrows on either side of it point at it.
Page built: 2025-10-17 using R version 4.5.0 (2025-04-11 ucrt)