Chapter 22 - A Gallery of Rogues: Other Methods

22.1 It Never Stops
The terrifying and delightful thing about research design is that there’s always more - new research designs, new estimation methods, new estimators, new adjustments, new critiques of old everything.667 Just think how much of this book will be outdated and known as bad advice in 20 years! None of it, actually. This book is perfect and eternal.
That’s what this chapter is about. The whole wide world of research design and causality is far too big to cram into one little book. What you’ve seen so far is me playing the hits. Difference-in-differences. Regression discontinuity. Everyone knows ’em, everyone loves ’em. They’re why you bought the concert ticket. But what about the new album or the b-sides?
It simply wouldn’t make sense to spend too much time on new methods. They’re untested! It’s simply impossible at this point to know which ones will stand the test of time and which will fall by the wayside. And even the ones that will be around a decade from now almost certainly aren’t in their final form yet. The chapter would be immediately outdated.
This chapter, however, is about methods that are either new, or developing, or just super interesting but a bit too technologically complex to try to teach them in this book. I’m not going to go deep into detail on them. No deep dive into caveats and details, no code examples (although I may recommend a few packages you can look into on your own). This chapter is about starting you on a journey of exploration. I’ll tell you what’s out there. I’ll give you an idea of how it works. And if it sounds interesting to you, you’ll have some sources to follow up on.
Let’s get going.
22.2 Other Templates
In this section, I’ll discuss a few promising template research designs. That is, they’re research designs that have a chance of applying in many different contexts, much like difference-in-differences, instrumental variables, and the other methods I’ve devoted whole chapters to in the second part of this book. Perhaps in some revision of this book, one of these will become a breakout star and get its own chapter and dressing room.
22.2.1 Synthetic Control
Synthetic control is the closest thing to another chapter that this book got.668 Or at least it was in the first edition. Now that the second edition has a different additional chapter, I guess this was a big stinky lie. It’s already well-established, popularized in Abadie, Diamond, and Hainmueller (2010Abadie, Alberto, Alexis Diamond, and Jens Hainmueller. 2010. “Synthetic Control Methods for Comparative Case Studies: Estimating the Effect of California’s Tobacco Control Program.” Journal of the American Statistical Association 105 (490): 493–505.), but around before that, and showing up in many places since then. However, it’s still enough on the fringe that it wouldn’t quite be considered a standard part of the toolbox yet, at least not to the degree something like regression discontinuity is. Maybe it will get there.
Synthetic control is sort of like a variant of difference-in-differences with matching (Chapter 18). We have the same basic setup as difference-in-differences: there’s a policy that goes into effect at a particular time, but only for a particular group.669 And in the case of synthetic control, it’s specifically one group getting treated, not an arbitrary number as in DID. That said, if you have multiple treated groups, there are ways of running synthetic control on each of them separately and aggregating the results. You use data from the pre-treatment period to adjust for differences between the treatment and control groups, and then see how they differ after treatment goes into effect. The post-treatment difference, adjusting for pre-treatment differences, is your effect.
So then, what’s the difference? A few things:
- Unlike with difference-in-differences, those pre-treatment difference adjustments are not done with regression, but rather by matching. Plus, unlike DID with matching, the purpose of matching is to eliminate these prior differences in outcomes, not to account for the propensity to be treated.
- Synthetic control relies on having many pre-treatment periods.
- After matching, the treated and control groups should have basically no pre-treatment differences. This is often accomplished by including the outcome variable as a matching variable.
- Statistical significance is generally not determined by figuring out the sampling distribution of our estimation method beforehand,670 Although there are ways of doing that, as in Chernozhukov, Wuthrich, and Zhu (2018Chernozhukov, Victor, Kaspar Wuthrich, and Yinchu Zhu. 2018. “A t-Test for Synthetic Controls.” arXiv Preprint arXiv:1812.10820.). but rather by “randomization inference,” which is a method of using placebo tests to estimate a null distribution we can compare our real estimate to.671 Specifically, you estimate your synthetic control effect. Then you drop your actual treated observation and cycle through all your control observations, estimating synthetic control estimates for each of them as though they were the treated group. This gives you a null distribution of treatment effects for untreated observations. Finally, check what percentile of the null distribution your actual effect is. If it’s far in the tails of the null distribution, that’s a good indication your effect wasn’t just random chance.
Synthetic control starts with a treated group and a “donor set” of potential control groups. Using the pre-treatment data periods, it implements a matching algorithm that goes through all the control groups and assigns each of the potential controls a weight. These weights are designed such that the time trend of the outcome for the treated group should be almost exactly the same as the time trend of the outcome for the weighted average of the control group (the “synthetic control” group).
Let’s see how this looks in data from Abadie and Gardeazabal (2003Abadie, Alberto, and Javier Gardeazabal. 2003. “The Economic Costs of Conflict: A Case Study of the Basque Country.” American Economic Review 93 (1): 113–32.).672 Surely my choice of this data has nothing to do with it coming already prepared and ready for use with synthetic control in the R Synth package, with code already put together in the help files. Perish the thought. This study looks at an outbreak of violent conflict in the Basque region of Spain in the late 1960s to see what effect the conflict had on economic activity. It compares growth in the Basque region to growth in a synthetic control group. Not too surprisingly, they find that GDP in the region was negatively impacted by the conflict.
Abadie and Gardeazabal match the Basque region to seventeen other nearby regions. The synthetic control algorithm creates weights for each of those seventeen regions in order to make prior trends equal, using information about those prior trends as well as other matching variables including population density, education, and investment levels. Conflict started around 1970, although it didn’t really kick into gear for a few years. So matching is done only on the basis of data up to 1969. Cataluna and Madrid turn out to be the strongest matches and get the most weight, with the other regions getting very little weight. These same weights are then applied across the entire time period.
The results of the matching process can be seen in Figure 22.1. As we’d expect, the values of the outcome are very similar in the pre-treatment period for the treated and synthetic control group. It sure looks like we’d expect them to continue to be the same in the absence of any treatment. Reassuringly, they continue to trend very closely together for a few years after treatment starts, but before the conflict really gets going. We’re not actively matching here (nothing’s forcing the lines to stay together), but they stay together nevertheless in a time period where the treatment intensity was very low. That’s good!
Figure 22.1: Synthetic Control Effect of Conflict on Basque Country Economic Growth, from Abadie and Gardeazabal (2003)
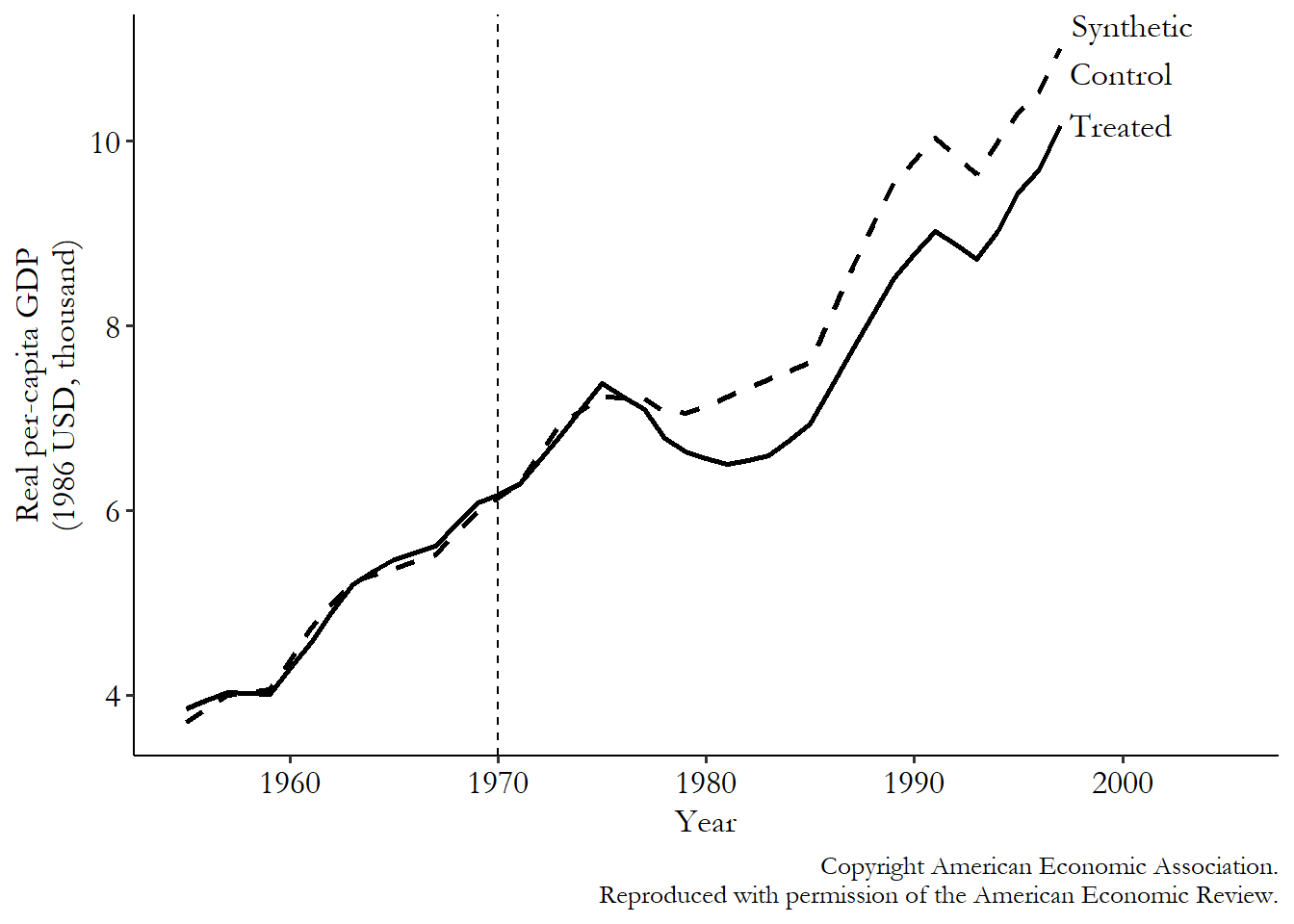
Then, the conflict really ramps up. At the same time we see the treated group and the synthetic control start to diverge, with GDP dipping lower for the Basque Country than for its synthetic control. Sure looks like the conflict is having a negative effect!
Like anything, synthetic control has its pros and cons. Its benefits in comparison to difference-in-differences are obvious. It doesn’t need to rely on that iffy parallel trends assumption like difference-in-differences did (it sorta forces the assumption to be true, or at least forces prior trends to be true, by its method). It makes the process of selecting a control group a little more disciplined. And because it doesn’t rely on regression, it is not as sensitive to functional form issues as difference-in-differences is (and naturally shows you dynamic effects without having to trot out a bunch of interaction terms). It may well be the “most important innovation in the policy evaluation literature in the last fifteen years” (Athey and Imbens 2017Athey, Susan, and Guido W. Imbens. 2017. “The State of Applied Econometrics: Causality and Policy Evaluation.” Journal of Economic Perspectives 31 (2): 3–32.), and that’s coming from two of the authors of the next method in this chapter.
Why isn’t it more popular than it is, then?673 And it is fairly popular - it’s almost certainly the next-most-popular template design after the ones I’ve given their own chapters, despite being much younger. It’s not quite as widely applicable as difference-in-differences, since it relies on cases where you have access to a lot of pre-treatment data (otherwise, the matching quality, or at least your ability to check match quality, will get iffy). It does have a tendency to overfit any noise in the outcome variable when matching - that’s no good. Also, the fact that it matches on the outcome variable just feels fishy - like using the outcome itself to close back doors is cheating. This is a natural skepticism, and like any method, synthetic control comes with its own set of assumptions that have to hold. But it is important to keep in mind that it’s only matching on pre-treatment outcomes, not the post-treatment outcomes where you actually estimate the effect. Plus, other methods like difference-in-differences also use information about pre-treatment outcomes to produce their estimate. They just do so in less obvious ways. Synthetic control isn’t pulling a fast one - you’ve been using pre-treatment outcomes all along.
If you are interested in learning more about synthetic control, I recommend the extended chapter on the method in Scott Cunningham’s Causal Inference: The Mixtape (Cunningham 2021Cunningham, Scott. 2021. Causal Inference: The Mixtape. Yale University Press.). Or for a bit more detail, Abadie (2021Abadie, Alberto. 2021. “Using Synthetic Controls: Feasibility, Data Requirements, and Methodological Aspects.” Journal of Economic Literature 59 (2).) covers cases when synthetic control works, and when it doesn’t. Synthetic control can be implemented in Stata using the synth package, often paired with the synth_runner package for easier use. In R, there is both the tidysynth package, which is a bit easier to use, or gsynth, which has more flexibility in how the design works. In Python you can use the scpi package, which is also available for R and Stata.
22.2.2 Matrix Completion
Let’s swing all the way from one of the most-established methods in this chapter to one of the least. Matrix completion is fairly new of this writing, making its debut in Athey et al. (2021Athey, Susan, Mohsen Bayati, Nikolay Doudchenko, Guido W. Imbens, and Khashayar Khosravi. 2021. “Matrix Completion Methods for Causal Panel Data Models.” Journal of the American Statistical Association, 1–41.), and despite that year of publication, it was around for about five years before that.674 Academic publishing is weird. I also happened to see this method presented in a seminar in Los Angeles in maybe 2017 or 2018. As I write this, the coronavirus pandemic is still ongoing. Geez, I miss seminars. I miss classrooms. I even miss Los Angeles, so you know I’m really desperate. But it is very promising, and the first of a few causal inference innovations derived from machine learning you’ll see in this chapter.
Matrix completion works with panel data, where you observe the same units over multiple time periods. In your panel data set, for a given individual (person, firm, country, etc.) in a given time period, that observation is either treated or untreated. We don’t just observe whether that observation is treated or untreated, but also we observe their outcome \(Y\). Simple enough so far.
But what about that outcome \(Y\)? It’s not just any outcome. It’s specifically the outcome that observation gets conditional on its treatment status. Say the treatment is that you watched the movie Home Alone on Netflix in a particular month, and the outcome is you choosing whether to watch My Girl, another Macaulay Culkin movie, on Netflix in that same month when given the chance. If you saw both movies, then your individual outcome is that you did watch My Girl that month conditional on having watched Home Alone. We have no idea whether you would have watched My Girl if you hadn’t watched Home Alone.
We can imagine a matrix (spreadsheet, basically) of outcomes. Each column is a time period, each row is an individual, and each element/cell of the matrix is your outcome. If you watched My Girl that month, then your outcome is 1, so that month’s column of your row would get a 1. If you didn’t, it gets a 0.675 The matrix completion method is not limited to binary outcomes.
But we don’t just have one matrix, we have two. We have one matrix conditional on you getting the treatment (watching Home Alone) and a separate matrix conditional on you not watching Home Alone. And - here’s the kicker - if we’re looking in the “treated” matrix in your row, in a month you didn’t get treated, then we have no idea what your outcome is conditional on getting the treatment, since you didn’t get the treatment. So instead of a 1 or a 0 for your outcome, you get a big ol’ “?”. We don’t know what your outcome would be if you’d gotten treated, since you weren’t treated. We’d love to compare your treated self to your untreated self to see how you were affected, but we can’t because we never observe both at once.
This whole idea - where the outcome you would have gotten is thought of as a missing value we’d love to compare to but can’t - is a pretty pure application of the potential outcomes model, which is another way of representing causal relationships besides causal diagrams.
Table 22.1: Table 22.2: Outcomes for Treated and Untreated Individuals
| Untreated | Treated | ||||||
|---|---|---|---|---|---|---|---|
| Ind | Time1 | Time2 | Time3 | Ind | Time1 | Time2 | Time3 |
| 1 | 1 | 0 | 1 | 1 | ? | ? | ? |
| 2 | ? | 1 | ? | 2 | 0 | ? | 1 |
| 3 | 1 | ? | 1 | 3 | ? | 0 | ? |
| 4 | ? | ? | ? | 4 | 1 | 1 | 0 |
One example of these matrices can be seen in Table 22.1. Individual 2 was treated in periods 1 and 3, so we see in the Treated matrix that their outcomes in periods 1 and 3 were 0 and 1, respectively, but period 2 gets a “?.” In the Untreated matrix, we only see the outcome for period 2 - a 1 - since that’s the only period they’re untreated.
Matrix completion is all about filling in ?s to complete the matrix. Specifically, it needs an untreated comparison unit for every treated observation, and so it tries to fill in the ?s in the Untreated matrix. If we can do that, in other words getting our best guess of what would have happened to all the treated observations if they’d been untreated, we can compare those outcomes to the ones they did get while treated.676 You could theoretically expand this to fill in values in the Treated matrix, or to use information from Treated to fill in Untreated, but for now the method is focused on scenarios where you only have a few treated observations, so that isn’t as useful. If you were treated and did see My Girl, but we predict that you wouldn’t have seen My Girl that month if you hadn’t been treated, then seeing Home Alone had a positive effect on your My Girl-watching outcome. Average together the estimated treatment effects over all the treated observations to get an average treatment on the treated.677 Or you can stop yourself before aggregating fully to look at things like how the treatment effect changes over time, or how varied it is across individuals.
How can we predict what those ?s would have been? We use the other data in the Untreated matrix. For example, in Table 22.1, we can see that for Individual 3, their Untreated outcomes in periods 1 and 3 are both 1, which makes it more likely that the ? in period 2 for Individual 3 would also have been 1 if we’d observed it. Similarly, in period 3, Individuals 1 and 3 both got 1s, making it seem more likely that Individuals 2 and 4 also would have had 1s if they’d been untreated. This is conceptually sort of like a two-way fixed effects model with fixed effects for both individual and time. Sort of.678 Like two-way fixed effects, matrix completion can be applied wherever a difference-in-difference design could be applied, but it works better than two-way fixed effects when the treatment timing is staggered, for reasons discussed in Chapter 18.
That’s the rough idea, but the application is a bit more complex than that. Crucially, it uses regularization, as we talked about in Chapter 13, to improve its prediction powers when filling in the matrix. Also, so far I’ve talked about using outcomes from other parts of the matrix to fill in ?s, but you could also use covariates to develop something like matching weights that would tell you how useful each other cell is in predicting your ?. Like with regression and matching, identifying a causal effect using matrix completion requires that the treatment is random conditional on whatever you use to create comparison weights.
If this sounds like an oversimplified description of the method, it is. The technical details do ramp up here quite quickly. But you’re about 80% of the way there (and only slightly incorrect) if you think of it as “using regularized regression to predict missing Untreated values, and then comparing the actual Treated values to those predictions in order to get an average treatment on the treated.”
Applications of matrix completion are few and far between, with more papers written on improving or understanding the method than using it. That’s fair - you don’t want to write a whole paper using a new method only to find out a year later something has been discovered and the method doesn’t work!
One application is G. Wood, Tyler, and Papachristos (2020Wood, George, Tom R. Tyler, and Andrew V. Papachristos. 2020. “Procedural Justice Training Reduces Police Use of Force and Complaints Against Officers.” Proceedings of the National Academy of Sciences 117 (18): 9815–21.). The authors in this paper are interested in the use of force by police officers, and whether a training course on procedural justice methods - which encourage respect, neutrality, and transparency in the course of police work - can reduce the use of force.
The authors look at Chicago, which got thousands of police officers to take the course. Treatment was staggered, with different officers receiving treatment at different times. They then checked whether the officer in question received complaints or used force on the job. Of course, we can’t see what amount of complaints they would have gotten, or force they would have used, without the training, but we can use matrix completion to guess.
They find that the training reduced complaints by 11% and the use of force by almost 8%. Not bad! Sure, they don’t have a lot of ways for controlling for officer characteristics in regards to who accepts the training. But matrix completion does allow them to see that each officer’s reductions in complaints and force seems to be timed to when they got the training, rather than just reflecting preexisting changes.
Matrix completion can be implemented in R using the estimator = "mc" option in the gsynth() function in the gsynth package.679 Wait, wasn’t that the package I suggested for synthetic control? Yep! Turns out matrix completion is a super general idea and synthetic control, difference-in-differences, and a few other designs are actually special cases of matrix completion. In Stata you can use the method("mc") option for fect in the fect package, and in Python there is the causaltensor package.
22.2.3 Causal Discovery
Oops, I lied. Remember all that business from the first part of this book about needing to use theory and experience to come up with a causal diagram that you could then use for identification? Sure, you could use data to show that you had the wrong diagram - a diagram might imply that two variables are unrelated; so if they’re related in data, your diagram is wrong - but data could never tell you what the diagram should be in the first place. Or could it?
Causal discovery is the process of using data to develop causal diagrams. How can this be possible? How can we possibly use data to uncover a causal diagram when we know that a given data set must be consistent with lots of different causal diagrams? There’s no one answer to that, as there are many different algorithms and processes for performing causal discovery - it’s more a general idea than a specific method. But let’s look at a classic (albeit slow) implementation, the SGS algorithm (Spirtes et al. 2000Spirtes, Peter, Clark N. Glymour, Richard Scheines, and David Heckerman. 2000. Causation, Prediction, and Search. MIT Press.).
We start the SGS algorithm with the set of relevant variables for our diagram. Let’s say we have four variables, just called \(A\), \(B\), \(C\), and \(D\).680 This example was considerably refined after reading Leslie Myint’s lecture notes.
To build a causal diagram from these variables, we have two tasks ahead of us. First, we need to figure out, for each pair of variables, if there’s a direct arrow between them. Second, once we know where the direct arrows are, we need to figure out which direction those direct arrows point.
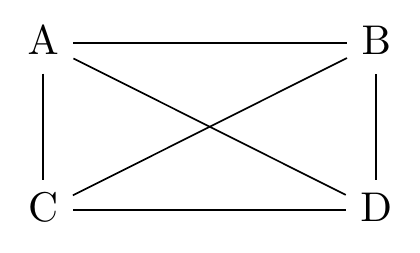
Let’s tackle the first problem. How can we figure out whether there’s a direct arrow (of either direction) between two variables? We check for conditional associations in the data. Simple as that. We start with a completely agnostic diagram in Figure 22.2, where every pair of variables is connected (note the lack of arrowheads - we don’t know what direction these arrows run).
Figure 22.2: A Diagram Where Everything Is Related to Everything Else
Let’s consider that line between \(A\) and \(B\). Should it be there? How can we tell from the data alone? Well, if there’s a direct line between \(A\) and \(B\) in either direction, then we should see a nonzero relationship between \(A\) and \(B\) no matter what we control for.681 This requires some decision process of what counts as zero. Statistical significance could be one, although there are other reasons besides a true zero that something could be insignificant. So, first we just look at the relationship between \(A\) and \(B\). If that’s zero, no direct line! But if it’s not zero, try controlling for stuff. Control for \(C\). Control for \(D\). Control for \(C\) and \(D\). If any of those sets of controls shuts off the \(A\) to \(B\) relationship, that means that the relationship they do have is blockable by some set of controls, which wouldn’t be possible if there was a direct line between them.682 This process assumes that the average effects we’re estimating here are representative. For example, if the effect of \(A\) on \(B\) is positive in half the sample, but negative in the other half, those effects might cancel out to give an average estimated effect of 0, telling us there’s no arrow when there actually is one. We must assume this doesn’t happen.
Repeat this process for each pair of nodes. Any relationship that can be set to zero by the use of controls is one more arrow you can knock off.
Figure 22.3: A Causal Diagram After Deleting Several Direct Arrows with Causal Discovery
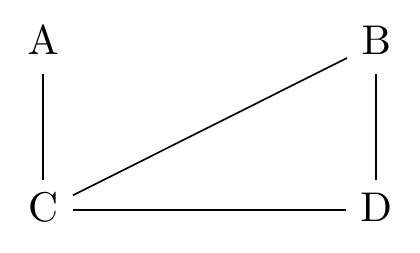
Let’s say that we did this whole process and what we ended up with was Figure 22.3. We’re already on our way.
Next, we’ll want to figure out which direction the arrows point. For this, we can head all the way back to Chapter 8 to think about colliders. Remember, if there’s a path \(X \rightarrow Y \leftarrow Z\) on a diagram, where both of the arrows are pointing at the same variable (\(Y\) here), then that path is pre-closed without any controls, but if we control for the collider, it opens back up.
Let’s apply this to Figure 22.3. In particular let’s look at the path \(A-C-B\). This path could be filled in a few different ways: \(A\rightarrow C \rightarrow B\), \(A\leftarrow C \leftarrow B\), \(A\leftarrow C \rightarrow B\), or \(A\rightarrow C \leftarrow B\).
What we want to do at this point is look at the relationship between \(A\) and \(B\) both while controlling for \(C\) and not controlling for \(C\).
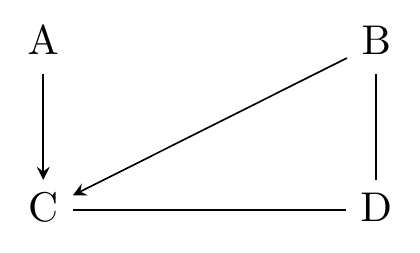
What could this tell us? If we observe that without a control for \(C\) there’s zero relationship between \(A\) and \(B\) and also with a control for \(C\) there’s a nonzero relationship between \(A\) and \(B\), then there’s only one thing it could be - a collider! So if we do find that, it must be \(A\rightarrow C \leftarrow B\). Now we have some arrows, shown in Figure 22.4.
Figure 22.4: A Causal Diagram After Discovering C is a Collider between A and B
But what if we don’t get that? Let’s say we want to finish out our diagram and so check the \(C-D-B\) path. This time we get a relationship between \(B\) and \(C\) whether or not we control for \(D\). This could be consistent with \(C\rightarrow D \rightarrow B\), \(C \leftarrow D \leftarrow B\), or \(C \leftarrow D \rightarrow B\).683 How is it consistent with these? Wouldn’t controlling for \(D\) shut down the relationship in all of these? It would, except that we also have the \(B\rightarrow C\) arrow outside of this particular path.
When we come to a case like this, we might still be able to progress - perhaps solving some other part of the diagram would let us determine \(D \rightarrow C\) and thus narrow down our options. But also we might have run into an equivalence class - a set of diagrams that our data can’t distinguish. Sometimes causal discovery can only get us part of the way there. So we’ll stay with Figure 22.4. Still, we know more than we did at the start. Maybe other methods, or bringing in some intuition and theory like normal, could help us narrow down the options.
So that’s your start in the world of causal discovery. We can ask the data what the causal diagram should be, and then once we have the diagram we can ask the computer how to identify it. Who knows, maybe the whole process will get so effective that we won’t even need any people to do causal inference, and this whole book will have been a waste of everyone’s time.
This description of the algorithm leaves out how causal discovery deals with things like unmeasured variables, and also plenty of other approaches to the problem, some of which use timing to narrow down the potential graphs, or changes in the graph itself to figure things out, not to mention all the massive speed improvements. Several causal discovery algorithms can be implemented in R using the pcalg package, or in Python using the Cdt package. There’s lots of cool stuff in this literature, and some of the algorithms are really ingenious. There are even algorithms that don’t require you to settle on any one causal diagram, and let you consider a whole bunch of possible diagrams at once, weighting them by how likely they are (Castelletti and Mascaro 2021Castelletti, Federico, and Alessandro Mascaro. 2021. “Structural Learning and Estimation of Joint Causal Effects Among Network-Dependent Variables.” Statistical Methods & Applications 30 (5): 1289–1314.), which can be implemented in the R package BCDAG.
22.2.4 Double Machine Learning
A lot of these methods are pretty brain-busting. Let’s kick back with something considerably more straightforward and familiar. Double machine learning (also known as debiased machine learning) is just another way to close back doors, like regression or matching (Chernozhukov et al. 2018Chernozhukov, Victor, Denis Chetverikov, Mert Demirer, Esther Duflo, Christian Hansen, Whitney Newey, and James Robins. 2018. “Double/Debiased Machine Learning for Treatment and Structural Parameters.” The Econometrics Journal 21 (1).).
Let’s think back to a basic regression setup. We want to know the effect of treatment \(X\) on outcome \(Y\). We’re in a setting where if we simply regress \(Y\) on \(X\), our causal diagram tells us that we won’t identify the effect of \(X\) on \(Y\). So we need to include some control variables. For simplicity, let’s just say we only need two control variables to close all the back doors: \(W\) and \(Z\). Then, we can identify the effect of \(X\) on \(Y\) with the regression equation
Simple! But then we remember the whole idea of what happens when we include a control variable - we’re removing the variation in both \(X\) and \(Y\) that is explained by the controls, and thus the part of their relationship that is explained by the controls. This closes any back doors through the controls, hopefully just leaving us with the front-door paths we want. This is how we described controlling for variables in Chapter 4.
As you might expect given this interpretation, we can get the exact same estimate for \(\hat{\beta}_1\) as in Equation (22.1) by removing the variation in \(X\) and \(Y\) explained by the controls ourselves:684 These steps are just a regression-based version of the same steps from Chapter 4.
- Regress \(Y\) on the controls \(W\) and \(Z\), and calculate the residual values of \(Y\), \(Y^R\). Remember, the residual values are the actual value minus the predicted value from the regression, \(Y - \hat{Y}\). This residual has removed all parts of \(Y\) that can be explained by the controls.
- Regress \(X\) on the controls \(W\) and \(Z\), and calculate the residual values of \(X\), \(X^R\). These residuals, too, have been scrubbed of all parts of \(X\) explained by the controls.
- Regress \(Y^R\) on \(X^R\).
Here’s where the double machine learning comes in. It looks at this list of instructions and asks the question: “uh… why does it have to be regression?”
The process for double machine learning is simple. First, predict \(Y\) using your set of control variables somehow and get the residuals \(Y^R\). Then, predict \(X\) using your control variables somehow. Finally, regress \(Y^R\) on \(X^R\) and get your effect.685 There’s also a version of double machine learning that is only slightly different and applies the same trick to instrumental variables estimation.
The somehow is where the “machine learning” part comes in. You just use a machine learning algorithm to do the predicting of \(Y\) and \(X\) using your controls, instead of regression. That’s it! It really could be any prediction-based machine learning algorithm. Regularized regression like we talked about in Chapter 13 is one option. As is the random forest, which will get a brief introduction later in this chapter. So is a bunch of stuff you’ll need a different, machine learning-focused book to read about. Neural nets, boosted regression, and the fifteen other new ones they came up with while I was writing this sentence.
There’s slightly more to double machine learning than just that, but not much - it also employs sample splitting to avoid overfitting. In its basic form, it splits the sample randomly into two halves. Then, it fits its machine learning model using only one half (half A), and then applies that model to get \(Y^R\), \(X^R\), and the resulting \(\hat{\beta}_1\) coefficient in the other half (half B). Then the halves trade places, fitting a model using B and using that to get residuals in A. Then average the coefficients from your two samples to get an effect.
Why would you want to do double machine learning? The problem with applying machine learning methods to causal inference is that they’re usually designed to be good at prediction, not inference (statistical or causal). But they are really good at prediction! Double machine learning finds one step in a standard causal inference design that is, inherently, a prediction problem. Then it gives that problem to a machine learning algorithm instead of a linear regression, so machine learning can do what it’s good at.686 This is also kind of the idea behind matrix completion, and many other machine-learning based causal inference methods.
Sometimes, linear regression is just fine. But sometimes it’s not. Machine learning methods are much better than linear regression when there are lots and lots and lots of controls (high-dimensional data), and also when the true model has lots of interaction terms or highly nonlinear functional forms. In these cases, double machine learning will do a better job fitting all those peculiarities than linear regression. Seems handy to me.
22.3 Modeling Heterogeneous Effects
It almost goes without saying that causal inference would be a lot easier if each causal effect were the same for everybody. If every treatment had the exact same effect on every individual, we wouldn’t need to worry about whether our results will generalize to other settings, or about which kind of treatment effect average our estimate has picked up. I could have cut Chapter 10 out entirely. But, alas, we live in a world of heterogeneous effects.
We can’t escape heterogeneous effects entirely, but we can give ourselves some tools to face them head on. Why not, instead of treating heterogeneous effects as some sort of nuisance where we have to figure out which average we’ve just drawn, we just estimate the distribution of effects? Then, not only could we take whatever average of that distribution we wanted, but we could toss out the average and look at the distribution overall. Sure, a mean is neat, but why wouldn’t we be interested in how the effect varies over the sample? What’s the standard deviation of the effect? The effect is bigger or smaller for who exactly? Is treatment more effective for old people than young? Poor than rich? French than Russian? And so on.
We’ve already dipped our toes into the water of estimating the heterogeneity in treatment effects. We talked about interaction terms in regression in Chapter 13. That’s one way to see how an effect differs across a sample, but it’s very limited - you can really only include a couple of interaction terms before your model turns into a poorly-powered impossible-to-interpret slurry.
We discussed hierarchical linear models in Chapter 16. These are much better than interaction terms in regression if your goal is understanding the full extent of the variation in an effect across the sample. In a similar way to how regression models an outcome variable as varying based on the values of our predictors, hierarchical linear models model coefficients as varying based on the values of predictors. If one of those coefficients is our effect of interest, we’ll get a decent idea about how much that effect varies, and who gets the strongest and weakest effects.
While we’re at it, let’s take a little peek at what else is out there. Research on the estimation of heterogeneous effects has been particularly active since the 2010s. One problem with estimating heterogeneous effects is that there are so many dimensions they could vary along. How could we check everything? But you know what’s good at checking everything and handling lots and lots and lots of interactions? Machine learning! The estimation of heterogeneous effects may well end up being machine learning’s most important contribution to causal inference. There are lots of these approaches. I’ll pick only one of these methods - causal forests, for being relatively straightforward to understand, easy to use, and likely to rank among the more popular options. But I want to be clear that there are zillions of such approaches, and more on the way. A good overview is available in Chapters 14 and 15 of Chernozhukov et al. (2024Chernozhukov, Victor, Christian Hansen, Nathan Kallus, Martin Spindler, and Vasilis Syrgkanis. 2024. Applied Causal Inference Powered by ML and AI. https://causalml-book.org/.).
It’s worth pointing out that these methods aren’t designed to identify an effect in some clever way. These assume that you already have a design for identifying an effect. But once you’ve identified the effect, these can help you see the entire distribution of that effect. You could just as easily use them to see the distribution of a non-causal association.
22.3.1 Causal Forests
We’re used to the idea of fitting a model, and then using it to make a unique prediction of the outcome for each observation. Simply regress an outcome on a bunch of predictors, then plug in the values of someone’s predictors to see what prediction the model spits out.
But what if we want to get a unique estimate of the effect of \(X\) on \(Y\) for each observation? That’s tougher. We don’t have a variable called “the effect of \(X\) on \(Y\)” in the data, so we can’t just do what we did for predicting the outcome. One thing we could do is estimate a model with interaction terms. If we regress the outcome on the treatment as well as the treatment interacted with other predictors, we can plug in the values of someone’s predictors to see what the effect of \(X\) on \(Y\) is for them. The problem with this is that regression simply can’t handle a lot of interaction terms, or highly nonlinear interactions. So we end up only using a few predictors to estimate differences in the effect on a pretty basic level.
Enter causal forests! Causal forests manage to take the task of estimating a unique effect for each individual, and morph it into a format that works basically the same as predicting the outcome in a certain non-regressiony way (Wager and Athey 2018Wager, Stefan, and Susan Athey. 2018. “Estimation and Inference of Heterogeneous Treatment Effects Using Random Forests.” Journal of the American Statistical Association 113 (523): 1228–42.). Our ability to handle lots of predictors and high degrees of nonlinearity then works just as well for estimating an individual’s effect as it does for predicting their outcome.687 In fact, not only can it handle lots of predictors, it actually has a hard time when there are only a few (say, three or fewer) predictors. If you only want to see heterogeneity across a couple of variables, causal forest is a bad pick.
How do causal forests manage this? To figure that out, I’ll need to start by describing the prediction method that causal forests modify to work for effect estimation - the random forest.
Random forests make predictions by splitting the sample. Imagine we were trying to predict how many hours of TV you watch per day, and we have only one predictor - whether or not you are married. In that case, it’s pretty obvious how we’d make our prediction. We’d split the sample and take conditional means. First, take the nonmarried people and get their average TV watching - let’s say it’s 3 hours per day. Then we take the married people and get their average TV watching - 4 hours per day. Now if we’re asked to make a prediction, we’d predict 3 hours a day for a nonmarried person and 4 hours per day for a married person. That’s simply the best prediction we can make with that predictor.
How about a different predictor? Instead of having marital status, our only predictor now is age. We can still make a prediction by splitting the sample in two, but now we have more choice. We could compare people age 6 and below to those 7 and above. Or 7 and below vs. 8 and above. Or 21 and below vs. 22 and above. Or 64 and below vs. 65 and above. Really, we could pick any age to split the data at. What’s the best prediction we can make? It’s whichever one most reduces our prediction error. Often this is measured as the sum of squared residuals. So if the sum of squared residuals when splitting the data by 21-and-below vs. 22+ is 4030.1, but the sum of squared residuals when splitting 64-and-below vs. 65+ is 3901.2, then the split at age 65 is a better one. We wouldn’t just pick a few cutoffs to compare, though; we’d try every possible cutoff and pick the best (lowest prediction error) option. So we try splitting at 2, and 3, and 4, and so on, all the way up to the oldest people in the sample. If the best cutoff really is at age 65, we use that. If the average below the cutoff is 2.7 and above the cutoff is 4.8, then we predict 2.7 for each person under 65, and 4.8 for each person 65+.
Nothing special so far, and as you can guess, just splitting the sample in two doesn’t get you very good predictions. There are still two steps to go before we get to a random forest though.
First is the step of creating a decision tree. A decision tree takes this sample-splitting idea and does it repeatedly. Now maybe you have a bunch of predictors to work with. Start by finding the best possible split for the sample by not just considering each possible cutoff level, but doing so for every predictor variable you have. So you check all the cutoffs possible across marital status, age, race, income, education, etc. etc. etc., and pick the best cutoff for the best variable. Then split the sample. Maybe age 64-and-below vs. 65+ does turn out to be the best split overall. Then we can draw a tree describing our split like in Figure 22.5.
Figure 22.5: A Decision Tree with a Single Split
We’re not done! Like I said, splitting the sample in two doesn’t get you far. So we split it again. Take just the 64-and-below split and repeat the process of finding the best cutoff for the best variable for them. It might even be age again. Let’s say it’s marital status. Now we head over to the 65+ split and do the process again for them. Let’s say the best split for them is income above $65,324 or below. Now our tree looks like Figure 22.6. Our sample is split into four distinct groups: non-married 64-and-unders, married 64-and-unders, 65+ who earn less than $65,324, and 65+ who earn $65,324 or more.
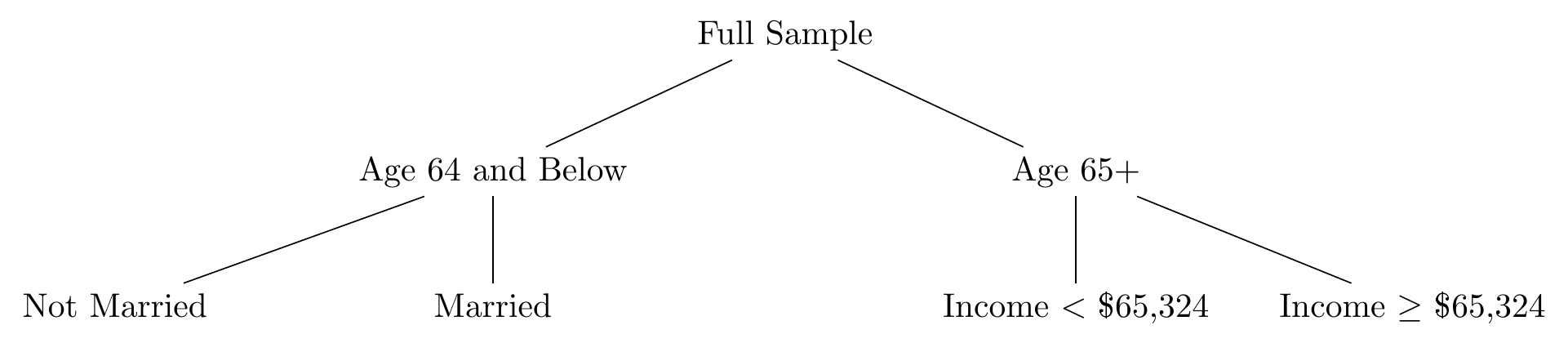
Figure 22.6: A Decision Tree with Two Splits
And we keep going. Keep splitting the sample over and over, finding the best split each time, until the sample we’re splitting gets to some definition of “too small,” and you stop there. Now we have a decision tree. My prediction for you is whatever the mean is in your split.688 There are other options besides taking the mean in your split, but let’s keep it simple. Also, notice by the way that it’s very easy to use random forest with a categorical or binary outcome. Random forest is often used for “classification” problems, i.e., predicting categories. So if you’re a 36-year-old Asian married person with a community college degree making $43,225, I make your prediction by following the splits down the tree until I find the small group of people very much like you. Then I take the mean, and that’s my prediction.
How do we get from a decision tree to a random forest? Add a bunch of randomness! First off, we bootstrap the whole process, like in Chapter 15, and create a decision tree for each sample. We create that decision tree with a bit of a difference, too: each time we try to split the sample, we don’t actually consider all the variables. We consider a random subset of the predictor variables instead (choosing a different random sample every time we split), and only look for the best split among those.
Once we’re done, we have a whole bunch of decision trees, each different and with its own predictions for each individual. The randomness we injected into the process helped make sure the predictions were as independent as possible, so no observation or predictor could be overly influential. The many predictions for each observation can then be averaged together to create a great prediction, taking advantage of the wisdom of crowds from these “independent” predictions.
That’s random forest. What is a causal forest? Causal forests are really just random forests but with a tweak. In a random forest, we chose splits for our data with a goal of minimizing prediction error, because we wanted to predict the outcome. In a causal forest, we want to see variation in the treatment effect. So instead, we choose splits based on how different the estimated effect is in each side of the split.
Let’s say we are still looking at TV watching. But now we want to see heterogeneity in the effect of “cord-cutting” (cancelling cable TV and just using streaming services) on TV watch time.
Now when we’re considering a split of age 64-and-below vs. 65+, we estimate the effect of cord-cutting on TV watching among those 64 and below (however we estimate that effect - controls, instruments, etc.). Then we estimate the same effect among those 65+. We then check how different the effect is. Maybe cord-cutting increases TV watching by .5 hours for those below 65, but decreases it by 1 hour for those 65+. That’s a difference of \(1 - (-.5) = 1.5\) in the effect. We do the same thing across all other possible splits and choose the biggest difference.
Then, once the split gets small enough, we stop splitting. The estimate of the effect within your split is what we think the effect is for you. Then, as before, we bootstrap the whole thing and limit our choice of splitting variables each time. The overall estimated effect for you is the average across all those bootstrap samples.689 There are, for both random and causal forests, some steps I’ve left out. These are common machine learning “training/holdout” procedures related to using only part of your data to estimate the forest, and then estimating the effect only for the other part.
That’s about it! Once the process is done, we have an estimate of the treatment effect for each individual. The method is also capable of estimating standard errors for each of those individual effects.690 The neat thing about causal forests, as opposed to some other heterogeneous treatment effect methods in machine learning, is that causal forest estimates have a known sampling distribution, so you can easily use standard errors with them. Once you have the individual estimates, you can ask questions like “whose effects are highest, and whose are lowest?” or investigate the whole distribution of effects.
Causal forests can be estimated using the causal_forest() function in the grf package in R. In particular the grf package uses “honest” causal forests, which just means that the sample is split in half, with one half being used to make tree-splitting decisions, and the other used to estimate effects. In Python, honest causal forests can be estimated with econml.grf.CausalForest(). There is not currently an implementation in Stata.
22.3.2 Sorted Effects
Causal forests were just one representative from a huge and growing literature on the use of machine learning to estimate treatment effect heterogeneity. Now let’s cover a neat little approach that isn’t even particularly popular as I write this, but, let’s be honest, I like it so it’s in the book. That approach is the sorted effects method (Chernozhukov, Fernández-Val, and Luo 2018Chernozhukov, Victor, Iván Fernández-Val, and Ye Luo. 2018. “The Sorted Effects Method: Discovering Heterogeneous Effects Beyond Their Averages.” Econometrica 86 (6): 1911–38.).
Sorted effects is pretty darn simple. There are plenty of regression-based methods that already allow for treatment effect heterogeneity. Regressions with interactions are one of them. But also, many nonlinear regression models like logit and probit naturally have treatment effect heterogeneity, since the effect can’t be that big if your probability of having a dependent value of 1 is near 1 or 0.
Sorted effects simply takes models like that and says “Hey! Why not, instead of reporting average treatment effects with these models, you estimate each individual person’s treatment effect, which the model already allows you to do?” Then, once you have that range of estimates, you can present the whole range instead of trying to smush things together into an average. Then, you present the estimates from lowest to highest (i.e., sorted).
This seems… super obvious, to be frank. What makes this its own method? Three things. First, the designers of sorted effects managed to figure out, using bootstrapping, how to estimate the standard errors on these individual effects in an accurate way, and how to handle the noisiness in the tails of the effect distribution, both of which can be difficult. Second, they introduced a few methods for what you can do with the distribution of effects, including comparing who is in different parts of the distribution. Who is affected the most, and who is affected the least? Third, because this is an approach to treatment effect heterogeneity that lets you summarize that heterogeneity in a single dimension (the effect itself), it allows you to make models with more built-in heterogeneity. A regular model with a whole bunch of interactions would be impossible to interpret. But sorted effects would let you interpret it easily, and also provide standard errors that account for all the interactions.
Let’s see what sorted effects can do. Let’s head back to the data from Oster’s study in Chapter 4. In this study, Oster was interested in the effect of a short-lived recommendation for taking vitamin E on the chances that someone would take it. The main thrust of the study is that the people who respond to these recommendations are the ones paying the most attention to their health in general. So when the recommendation is on, it should look like vitamin E has all these great health benefits, simply because healthy people are most likely to respond to the new recommendation.
Part of her study was in establishing that people with other great health indicators were most likely to take up vitamin E in response to the recommendation. Oster had a few ways of doing that descriptively. Let’s see what sorted effects can do with a more structured approach.
We’re going to regress, in a logit model, the probability of taking vitamin E on being in a during-recommendation period. We’ll include as predictors (which we’ll also interact with treatment) whether they ever smoked, a standardized score of their exercise level, and a standardized score of their vitamin-taking behavior. The list could reasonably be much longer than that, but let’s keep it simple.
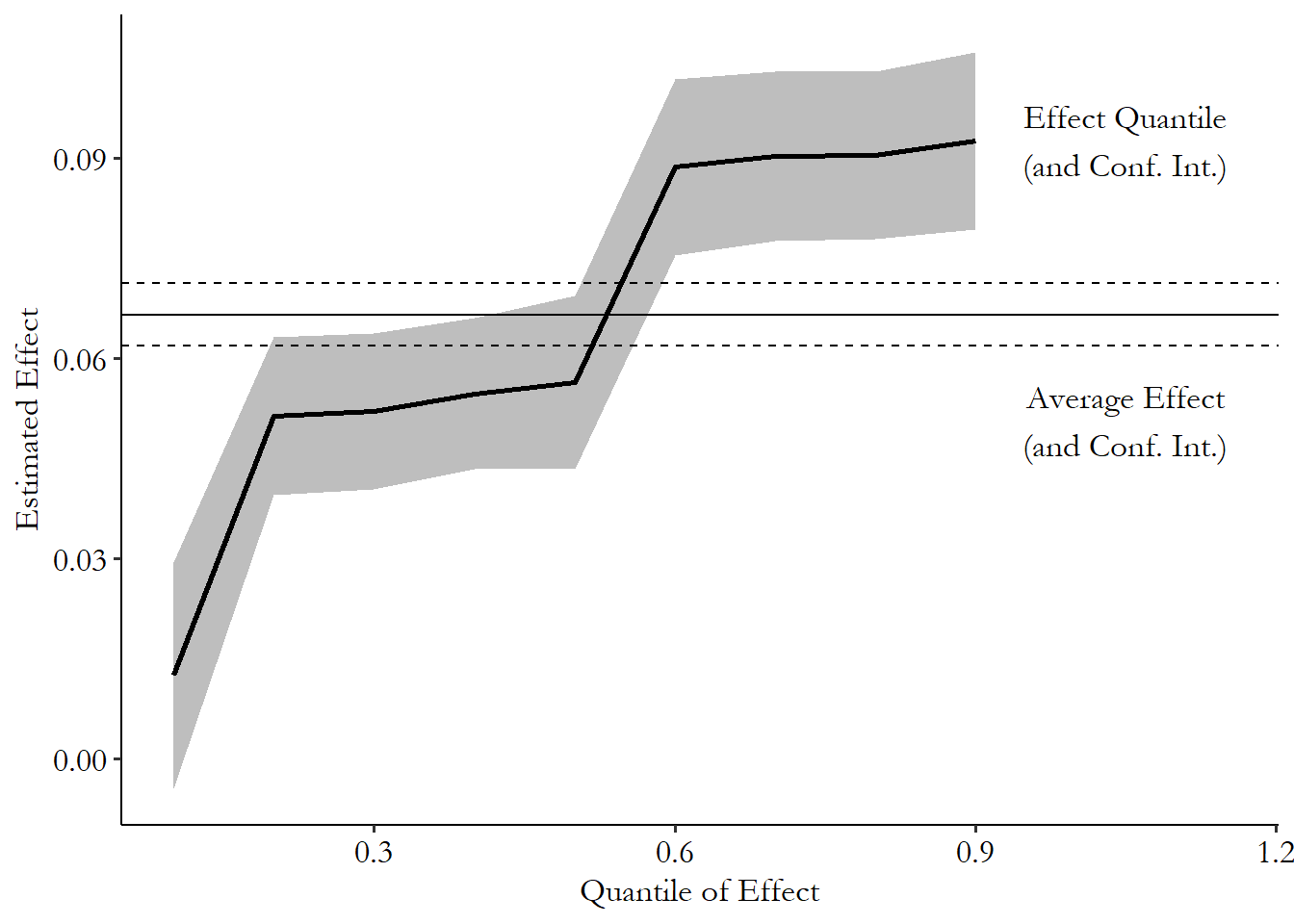
The sorted effects method estimates the distribution of effects, as shown in Figure 22.7. The average effect, while it’s more precise than any particular effect, leaves out a whole lot of the distribution. There are people in the data estimated to have effects much lower and much higher than the average. In fact, very few seem to be at the average, or even inside its 90% confidence interval. Who is it describing really?
Figure 22.7: Sorted Distribution of Effects of Vitamin E Recommendation on Taking Vitamin E
Sorted effects also lets us see who those people are. Table 22.3 shows the mean and standard deviation of the predictors in the model among those with estimated effects in the top 10% and bottom 10%.
Table 22.3: Characteristics of Those Least and Most Responsive to Health Recommendation for Vitamin E
| Variable | Mean | SD | Mean | SD |
|---|---|---|---|---|
| Smoking | 1 | 0 | 0 | 0 |
| Exercise Rating Score | -0.515 | 0.612 | 1.45 | 0.193 |
| Vitamin Behavior Score | -2.04 | 0.332 | 1.71 | 0.105 |
The differences are pretty stark. Smoking is the biggest tell. Among those who were estimated to be in the 10% least responsive to the vitamin E recommendation, literally 100% of them were smokers. And among the 10% most responsive? 0% were smokers! That’s a big difference. Maybe it’s not too surprising that people who smoke aren’t that responsive to recommendations from health officials, but I didn’t expect the difference to be 0 vs. 100!691 Although keep in mind this is just a demonstration of the method; you shouldn’t think of these results as being any sort of conclusive.
We also see differences for the exercise and vitamin behavior scores. Those who responded the most had considerably higher scores on both of these measures.
These results are pretty strongly supportive of the idea that people who already follow other health recommendations were more likely to follow the vitamin E recommendation, as Oster found. You can imagine, also, how this might be used to see how a given policy intervention might be more helpful to some people than to others.
The sorted effects method can be performed using the SortedEffects package in R.
22.4 Last But Not Least: Structural Estimation
Let’s finish things out with a little cherry on top. Throughout the first part of this book, I focused almost exclusively on attempting to map out the entire data generating process in a causal diagram. Then, we thought about identification in the form of shutting down back-door paths. Then in the second part, I walked that back a bit and have been talking mostly about methods designed to work even if you don’t have a firm grasp on the entire data generating process.
The first approach - thinking about the entire underlying model and figuring out from that how to estimate an effect - is known in economics as a structural approach.692 This is not to be confused with the method “structural equation modeling,” which has some similarities with this but is not the same thing. Structural approaches do require some strong assumptions - they only work if you are right about the underlying data generating process. But if you’re wrong about that, it’s not always clear what other methods actually tell you anyway. So why not take a structural approach?
That’s why I devoted the first part of this book, and many sections in the second part, to thinking structurally about your modeling and research design process. If we’ve covered it already, what’s this section on structural estimation about?
This section is about the fact that structural estimation doesn’t stop there. Using theory to figure out a list of control variables to add to a linear regression is a pretty limited way to do structural modeling. Someone doing structural modeling properly would not just use theory to determine a set of alternative pathways to consider, but would also see what kind of statistical model the theory implies.
For example, if we had a bunch of data on object masses and the gravitational force pulling them to other objects. We’d think about the underlying theoretical model, where the gravitational pull between two objects is \(F = G\frac{m_1m_2}{r^2}\), where \(m_1\) and \(m_2\) are the masses of those two objects, \(r\) is the distance between them, and \(G\) is the gravitational constant.
If we want to know the effect of \(m_1\) on \(F\), A basic approach would recognize that \(m_2\) and \(r\) may be alternative explanations for the relationship, and so you might end up running a model like \(F = \beta_0 + \beta_1m_1 + \beta_2m_2 + \beta_3r + \varepsilon\). This is not a great model. It ignores the actual way that the variables come together and all that theory you worked on. The effect of \(m_1\) on \(F\) shouldn’t be linear, and we know that from the theoretical equation. Structural estimation would hold on to the theory and would estimate the equation \(F = G\frac{m_1m_2}{r^2}\) directly. It’s the process of estimating the actual model implied by theory.
As a bonus, once you’re done, you know exactly which theoretical parameters relate to which estimated parameters.693 Imagine trying to figure out which combination of \(\beta_0\), \(\beta_1\), \(\beta_2\), and \(\beta_3\) represented \(G\) in that linear regression. In a structural model, you’d just estimate \(G\) directly. You’d know which coefficient represented \(G\) because it would be represented by that \(G\) you estimated. As another bonus, the structural process shows you exactly how to handle different unobserved theoretical concepts that you can’t actually measure.
Because structural models estimate theoretical parameters like \(G\) directly also means that it’s much easier to answer complex causal questions. Most of this book has been laser-focused on “does \(X\) cause \(Y\) and how much?” with only a few exceptions. But if you have a structural model, you immediately get access to how any variable in the model causes any other variable. And how that effect differs in different settings. And how the effect might change if we tried something completely new that isn’t even in the data. You have access to the whole model at that point (assuming, again, you have the right model). You can ask the model what’s going on; you don’t have to wait to see more data.
How can you estimate a whole theoretical model yourself? Structural estimation constructs statistical statements out of theoretical ones and uses those to estimate. For example, the gravitational equation I just used isn’t perfect; it leaves out quantum effects.694 And in a social science setting, we could easily imagine plenty of things left out of a model. So there is some error and we might claim it looks like this: \(F = G\frac{m_1m_2}{r^2} + \varepsilon\). If we are willing to make a claim about the distribution that \(\varepsilon\) follows, then we can pick values of our parameters (perhaps trying out \(G = 3\)) and see how unlikely our observed data was to occur given the model. We try a bunch of different parameter values \(G = 4, G = 5.3\), and so on, until we find the ones that best fit the data. This is estimating the structural model by maximum likelihood. You can do a similar process with other estimation methods like the generalized method of moments.
Now we come to the reason why I haven’t covered this yet. Simply put, the math gets hard! Drawing a causal diagram for your model doesn’t cut it - you need to specifically write out, and solve, the mathematical form of your model. Then you need to set up the statistical statements properly - remember, you have to do this all yourself, as the whole idea is that the estimation is unique to your model.695 That said, some mathematical forms do pop up a lot. Multinomial logit estimation comes up so commonly in structural estimation in microeconomics that some people casually think of them as being the same thing. Then you can finally estimate your parameters.
So that’s why I don’t go too deep into structural estimation in this book. However, if you’re interested and have the chops for it, I can recommend starting with Reiss and Wolak (2007Reiss, Peter C., and Frank A. Wolak. 2007. “Structural Econometric Modeling: Rationales and Examples from Industrial Organization.” Handbook of Econometrics 6: 4277–4415.), which is specifically about structural modeling and estimation in the economic subfield of industrial organization, but it does a good job at introducing the general concepts you’d use elsewhere. Galiani and Pantano (2021Galiani, Sebastian, and Juan Pantano. 2021. “Structural Models: Inception and Frontier.” National Bureau of Economic Research.) do a similar kind of introduction, focusing on labor economics.
Page built: 2025-10-17 using R version 4.5.0 (2025-04-11 ucrt)