Chapter 11 - Causality with Less Modeling

11.1 Confidence

Copy link

Everything we’ve done up to now when thinking about identifying a causal effect has started with the same idea: draw a causal diagram. Draw a causal diagram to map out our idea of the data generating process, use that diagram to list out all the paths from treatment to outcome, and then close pathways so that we are left with just the Good Paths we want. Then we’ve identified our effect!

So what if we can’t get that first step? What if the causal diagram itself is beyond our reach?

It’s not just sheepishness at not being willing to put our assumptions down on paper. In complex situations - and most social science is about highly complex situations - we may well not know very much about what the causal diagram looks like. Sure, we could draw a diagram, but it would have to be a massive simplification, and we’d likely not even think of all the important variables that should be on there. If we were being honest, we’d map out what we know, and then have a big space labeled “I DUNNO, SOME STUFF I GUESS” with arrows pointing from that to just about everything else on the diagram.

So what then? Do we just give up?

There are certainly some reasons why this very reasonable concern might turn us away from causal inference entirely. If we don’t know what large portions of the causal diagram look like, then we will likely fail to recognize important back doors that need to be handled. Or perhaps we will try to close a back door, but by accident open up a path instead because there’s a collider on it.

One approach we can take to this is to use the methods from Chapter 9, where instead of having to handle the mysterious mass that is “the entire set of back door paths,” we can instead just try to focus on isolating a few front doors we know are there.

However, outside of that there are still some options. We’ll never really, truly know what the actual causal diagram is. If we have a pretty good idea, we can just act as though that’s the truth.171171 There’s a good chance that we’ll learn later that we made a fatal flaw, but sometimes it’s hard to figure out how to do it better without making the mistake in the first place. Also, for now, this might be the best we can do. But if we know there’s a lot of unknown spaces on our graph, we can ask ourselves what we can do to identify our causal effect the best we can, while reckoning with our own lacking knowledge. Ignorance is inevitable; let’s make it not quite so painful.

11.2 Wide Open Spaces

Copy link

We’ve talked a lot about models. We’ve made complex models, we’ve drawn diagrams, we’ve carefully thought through the paths between treatment and outcome in a bunch of different directions. We’ve drawn messy models and clean models.

But for a lot of researchers, especially those who see the task of carefully modeling the data generating process as effectively impossible, the real model they’re working with is a lot less complex. Rather, it looks like Figure 11.1.

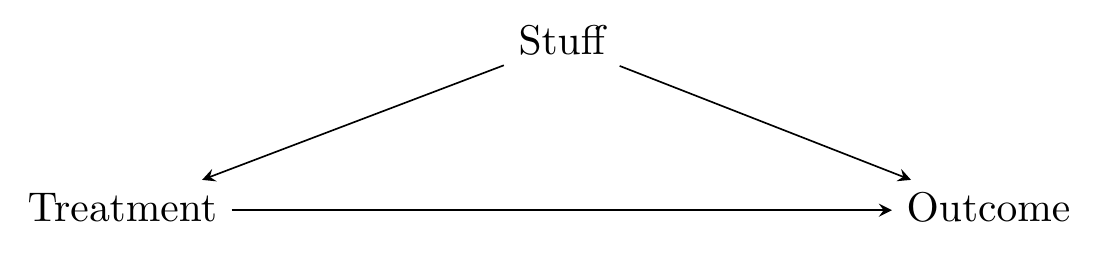
Simple, straightforward. Treatment, outcome, and a back door through, uh, something. Some stuff.

Despite being simple, this diagram is actually far more daunting. By just writing “Stuff,” we’ve given up even trying to figure out what all the back door paths are and how to close them. Sure, we can name a few things that might fall into the category of “Stuff,” but we’ll never name and measure them all.172172 In economics, this question of approach - whether to try to map out the whole data generating process or to throw up your hands, call it impossible, and try to do things some other way - is the “structural vs. reduced form” debate. This book up to this chapter has been largely in the “structural” camp. Not to say that I think the reduced form side is wrong - much of my own work is reduced form. But I think most reduced-form types would agree they’re doing as much structural work in their heads as they can before they face reality and switch gears for the actual analysis. That’s why I think the structural side is a good place to start learning causality, regardless of where you end up going. This is as opposed to most econometrics textbooks, which are heavily reduced form (perhaps because structural econometrics, as opposed to structural theorizing, is much more difficult than reduced form, and economics as a field has decided to teach research design and statistical inference at the same time for some reason).

This is a kind of principled ignorance. We know some things about what kinds of variables fit in “stuff,” but we recognize that we don’t know them all. Let’s take an econometric classic as an example - what’s the effect of an additional year of education on your earnings? We can be pretty certain that demographic and socioeconomic background variables go into “stuff,” as does intelligence, personality, the kind of school you’re in, and so on. But even if we wrote out a list of fifty things and managed to control for them all, we would still say “I don’t know everything, and the world is very complex. I must still be leaving something out. I don’t believe I’ve identified a causal effect yet.”

Unsurprisingly, people who think this way rarely believe that you can identify a causal effect just by controlling for variables.

So if we can’t see the whole DGP, what can we do? Well, we can try to fill in whatever we can. That can get us a long way.

Instead of trying to map out the entire process, we will instead imagine that the data generating process looks more or less exactly like Figure 11.1, and spend all of our time asking what variables belong in “Stuff.”

Surely the actual diagram isn’t quite as simple as Figure 11.1. We know that. But we can probably think of most bad paths as simplifying in some way to this. In other words, we know it’s a problem when some third variable causes both Treatment and Outcome. There are probably enough of those variables to use up all our energies anyway, so let’s just focus on that.

That’s the question, then - what variables out there likely cause both Treatment and Outcome? Don’t worry about how those variables might cause each other, don’t worry if there are potential collider effects going on, just worry about Stuff.

Let’s take an example. We are interested in the concept of remittances, which are money that immigrants send back to their families in the country they came from. We want to know whether, among immigrants, the country that you emigrate to affects how much you send back in remittances.

What might cause both “destination country” and “remittance amount”? Anything that relates to the kind of work you do is likely to be a factor - training, education, intelligence, strength, and so on, since these will affect both which countries you’re capable of emigrating to, and how much you earn once you get there (and thus can send back). The country you’re coming from is a factor for similar reasons, although in this case it might affect what you send back because of how much your family needs it. Your culture, language, or religion might play a part - perhaps people prefer to emigrate to countries with similar cultures, languages, or religions where they might find it easier to fit in, and these same factors might influence what you can earn, or what expectations your family places upon you for remittances.

We could go on, but this is a decent list so far. We can think of these as “sources of bias” - if we don’t control for them, we won’t identify the effect. We might accidentally include some variables in here that are colliders on some path, or that are actually irrelevant, but in general, asking “what variables cause both treatment and outcome” is on the easier end of the spectrum when it comes to laying out a causal diagram.

The key deviation at this point from the approach taken in the rest of the book is that we take this list of necessary controls and… don’t use it to identify the effect.

Sure, we might control for some of them. But under this approach, we can take for granted that if we haven’t already found a variable we can’t control for, then that just means we didn’t think hard enough about it. And if we think harder and do think of one, then either we can’t control for it and we’re stuck, or we can control for it and then we still have even more thinking to do.

Instead, this list of back-door fodder serves as a starting point. A set of considerations about the kinds of things we need to control for, but which we are going to control for indirectly, perhaps without controlling for anything at all.

How can we control for Stuff without controlling for Stuff? Well, we already know one way, and it might give you a hint for the other ways. In Chapter 9 we talked about how we can isolate just some causes of the treatment that are unrelated to the outcome.

If we can do this, then, in effect, we are controlling for Stuff without controlling for any Stuff at all. The back doors simply don’t matter! And when you’re thinking that there’s no way to properly treat and close all the back doors, then doing something that makes all the back doors not matter at once sounds pretty good.

If we’re doing this, why bother thinking about all the back-door Stuff in the first place? Because it encourages us to think about whether that exogenous source of treatment we need to find a front door is actually related to some of that Stuff - making it not so exogenous any more, or letting us know we do need to control for a little bit of Stuff too. In fact, we don’t even need to think about whether our exogenous source is related to Stuff, we can actually test it ourselves - I’ll talk about this in the next section.

The finding-front-doors method demonstrates that our goal here is to select methods that let us close a bunch of back doors at once, even if we can’t measure the variables on those back doors. But it’s not the only method for accomplishing this goal.

Sometimes, a control in the hand is worth an infinite number in the bush. Some controls are both easy to measure and can close a lot of back doors.

Keeping in mind that the idea of controlling for a variable means removing any variation explained by that variable, then by controlling for a variable we will also be controlling for anything else that only varies between values of the first variable.

That was confusing. Let’s try an example. Let’s say we’re doing a study on nature vs. nurture, and so to control for one aspect of nurture, we control for the house you grew up in - this would effectively result in comparing you against your siblings who grew up in the same house (or perhaps kids in other families in a multi-family household).

One other aspect of nurture we might want to control for is the geography of the region you grew up in - city vs. rural, the qualities of the neighborhood, and so on.

But once we’ve controlled for the house you grew up in, we don’t need to control for that other stuff. The other kids who grew up in your house with you also grew up in your neighborhood, in your state, in your country, and so on. Something like neighborhood only varies between different houses. Once we’ve removed all variation related to your house, that will as a matter of course remove all variation related to your neighborhood.173173 For there to be any variation in neighborhood left after controlling for house, there would need to be houses that were in two different neighborhoods at once. So we don’t need to control for neighborhood, or city vs. rural, or any number of other things that only differ between houses.

Most commonly, this comes up in the case of the method of “fixed effects,” where individuals are observed multiple times, and a control for individual is added. This effectively controls for everything about that individual, whether it’s easy to measure or not - their upbringing, their personality, and so on - as long as it’s constant over time.174174 So something about a person that changes over time, like their income, would not be accounted for by fixed effects. Plenty of controls knocked out in one fell swoop!175175 More about this method in Chapter 16.

Sometimes we can just assume things are comparable. Another approach that is often taken when there are far more controls that need to be added than are feasible is to take our group of treated people and compare them only to a group that is, by assumption, on average comparable on all these controls in some way. A control group! If we assume that something about these controls is identical between the treated and control groups, then we don’t need to control for any of them, since they’re already the same.

This approach of selecting a control group is standard when implementing an experiment. We enforce the comparability of the groups in that case by randomly assigning people to treatment or control. On average, there shouldn’t be any differences on any of the variables on the back doors, since we randomly assigned people without any regard for those variables. No need to add them as controls then.

In cases where we haven’t explicitly randomized, however, this is a much heavier assumption to take on. In pretty much any observational context, it would be completely unbelievable to just claim that the treated and untreated groups are the same for all variables on back doors, observable or unobservable. You’re basically just assuming you’ve identified the treatment effect at that point, without doing anything, on no justification.176176 Of course nobody would try to claim such a… ah, who am I kidding. Of course there’s a study that does exactly this getting huge press coverage and glowing politically-based praise as I write this, touting a coronavirus cure. Just straight up assuming that entire different countries are the same on average on all unmeasured back doors, and having the gall to call that a “country-randomized controlled trial” without even randomizing anything. Hello from 2020. If this book survives long enough that you have no idea what I’m talking about, I can only hope that your era-defining events are positive ones.

So do we really do that? Just assume that treatment and control are the same? No, of course not. Instead, we try to find particular comparisons of treatment and control that are the same.

This could be by finding a subset of the control group that really does seem like it should be the same on average for all of the Stuff, measured or not. For example, say you’re interested in the effect of receiving community-support funds from the government on the level of upward mobility in a community. Clearly, the communities that receive the funds are different from those that don’t, so we wouldn’t want to just compare treatment and control.

But perhaps we could make a case that among the communities that applied for funding, the communities that got funding are very similar to the ones that didn’t, with funding awards being semi-random. That’s not quite as good as actual randomization, but it’s certainly a start, and likely controls for a lot of variables we couldn’t measure, like “need for community funding.”177177 For a standard method that takes this sort of approach, see Chapter 20 on regression discontinuity.

Another way we could make particular comparisons is by comparing treatment and control not on average, but rather just within certain parts of the variation. For example, rather than asking whether the treatment outcome average is different from the control outcome average (a comparison for which all of those variables on back doors are very much still active), we can ask whether changes over time in the treatment outcome average are different from changes over time in the control outcome average.

By looking at changes over time in the outcome, instead of the absolute level, we make the treatment/control comparison a lot more plausible, since we don’t need the treatment and control groups to be the same on average for all the Stuff. We just need the change over time of that Stuff to be the same on average.178178 For a standard method that takes this sort of approach, see Chapter 18 on difference-in-differences. There are many other ways that we can knock out a lot of the variation in the Stuff, and rely on much narrower assumptions about what the treatment and control are comparable on.

So there are some saving graces available to us that we can use to identify an effect, even if we’re doubtful of our ability to truly map out the data generating process, or to ever figure out and measure the full set of necessary controls.

Each of these alternate approaches rely on their own sets of assumptions. And the whole idea here is that we didn’t want to have to make a bunch of strong assumptions about the data generating process! It sort of seems like, instead of having the principled ignorance to admit what we don’t know, we’ve just traded one set of assumptions for another.179179 This is unfair, but I am enjoying myself, so deal with it.

Thankfully, the researcher has yet another set of tools at their disposal that they can rely on to figure out whether their assumptions (which, if you remember from way way back at the beginning of the book, we have to have assumptions to identify anything) have indeed led them astray.

11.3 Yes, I’m Wrong, But Am I THAT Wrong?

Copy link

Here we are, an estimate to our name, a set of controls, perhaps a control group or a way of isolating front doors, and still skeptical, ever skeptical, that we’ve managed to identify what we think we’ve identified. How can we make ourselves more certain?

Testing whether our assumptions are true is rarely possible - they often aren’t about things we can observe in the first place. However, there are a few good avenues for checking whether our assumptions seem false. Distressingly, this is much easier to do (at least when it comes to checking assumptions using data rather than theory) than checking whether they seem true.

This brings us to the wide wide world of “robustness tests.” A robustness test is a way of either (1) checking whether we can disprove an assumption, or (2) redoing our analysis in a way that doesn’t rely on that assumption and seeing if the result changes.

One way of doing robustness tests we already covered in Chapter 8. In that chapter, we looked at a causal diagram such as in Figure 11.2.

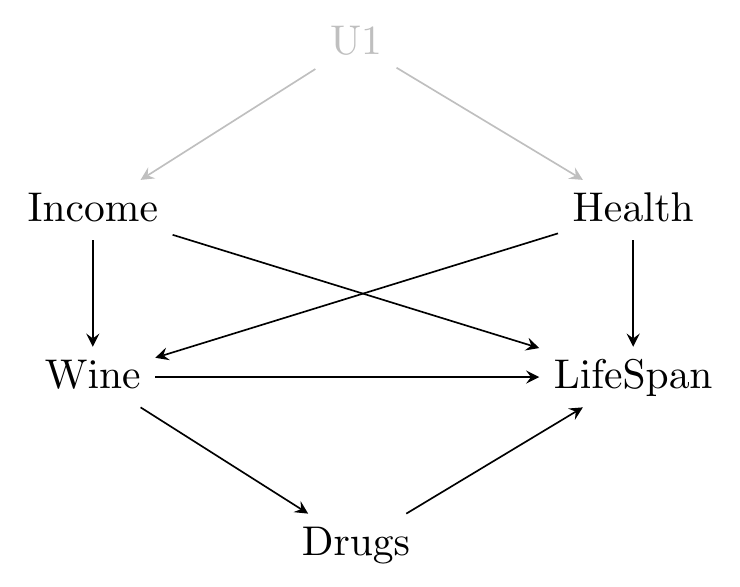
This figure doesn’t just imply what we need to control for in order to identify the effect of Wine on LifeSpan, it also exposes some assumptions we’re making. For example, all paths between Drugs and Income on this diagram either contain a collider or contain Wine. So we are assuming that if we control for Wine, Drugs and Income should be unrelated. If we control for Wine and they are related, then that’s evidence against one of the assumptions we made.

Most robustness tests work in a similar way to this. We detail an assumption we’re making, which usually implies that a relationship between two things is not there, and then we test it. If that relationship is there, then that’s evidence against our assumptions.

There are a whole bunch of available robustness tests for any given method you could be using. But let’s take an example. Let’s say we’re relying on a control group, where we’re comparing changes over time in the treatment group to changes over time in the control group.

Using this method assumes that the changes over time in all the back-door Stuff is the same in the treatment and control groups. So if we were to take some of those changes over time, we should find no relationship between changes over time and whether you’re in the treatment group or the control group.

Now we have the relationship that should not be, and we’re set up for our robustness test. We just need to take one of those back door control variables and see if its changes over time are related to being in the treatment or control group.

If that relationship is there, that’s evidence against the assumptions we made for our research design. Sure, we could just add that variable as a control to fix the problem with the variable we checked, but even if we do that, we still have all the unmeasured variables in Stuff to worry about. We were operating under the assumption that we’d solved that problem. But checking the variable we could check showed we didn’t fix it for that one, so why believe we did any better with the others?

Figuring out what kind of robustness test to do requires thinking carefully about the assumptions being made, and what sort of observable non-relationships those assumptions imply.180180 And, rarely, there are observable relationships that should be there that you could test and be concerned if they’re not there. That would be a robustness test too; this kind is just less common. Then the tense moment while you hope really, really hard to not find a result… and, well… we’ll see!

One form of robustness test that can help ferret out bad assumptions, especially when you are using a method that compares a treated group to a comparable control group, is the placebo test. A placebo test is, as you might guess from the name, a test where you pretend that treatment is being assigned somewhere it isn’t, and you check whether you estimate an effect. If you find an effect of “treatment,” that tells you that there must be a bad assumption somewhere, since you’re finding that the effect of nothing is something!181181 This is different from the use of actual placebos in medicine, where the placebo is expected to have an effect because we can react to the belief that we are being treated (among other things; placebos are complex), and we just want to know if the real treatment has an effect beyond that placebo effect. In our usage of placebos, the placebo treatment occurs only inside our statistics software after the data is all collected - nobody actually received a placebo treatment. The effect really should be zero. We discussed these before in Chapter 8 but they bear another look.

For example, say you’re looking at the impact of an environmental conservation letter. A certain county tested a policy where, if you used above 1,200 kwh of electricity in a given month, you’d get a letter asking you nicely to use less. We think that untreated people who use 1,151-1,200 kwh are a pretty good control group for the treated people who use 1,201-1,250 kwh. Those usage rates are so close that we’d expect those groups to be similar on all back-door Stuff variables we can or can’t measure. So we compare next month’s usage among those who had 1,201-1,250 kwh last month to those who had 1,151-1,200 kwh last month. That’s our design! Nice and simple.

A standard robustness-check approach here would just be to see if the Stuff variables we can measure are different between the 1,151-1,200 kwh and 1,201-1,250 kwh groups.182182 A table comparing a bunch of Stuff-type variables across the treated and control groups is often referred to as a “balance table.” Balance tables will show up again in Chapter 14.

However, we can also do a placebo test. Let’s imagine that the policy instead went into action at above 1,150 kwh. Now we can use the exact same design - this time comparing our fake-treatment group of 1,151-1,200 kwh against the new control group of 1,101-1,150 kwh. Now, there shouldn’t be a big difference between these two groups in their next month’s usage, because in actuality they both received the same treatment, which is no treatment at all. So if we do find a difference between these groups, that tells us that one of our assumptions is likely to be off. Perhaps groups whose usage differs by 50 kwh, in fact, are quite different on a lot of back-door-relevant variables!

To be honest, all of this is a little fanciful. The whole idea that we can test whether an assumption is true or not is silly. All assumptions are wrong at some level. We’re not so much trying to prove these assumptions true or false as we are trying to prove them “not so wrong as to cause problems” or “too wrong to work with.”

Do we have to do that? Surprisingly, no! There is another way. This is the partial identification approach.183183 Also known as “set identification.” The term “sensitivity analysis” is related, and, in fact, the example here is sensitivity analysis. At the level of this book I think the ideas are closely related enough to be treated as one, but there are differences between them, as you’ll find if you research further.

Under partial identification, we don’t force ourselves to keep making assumptions until we’ve identified the effect. Instead, we make the assumptions that we’re pretty certain about. Then, we use a range of possibilities about the remaining things we must assume. Finally, we figure out what our estimate is over that range, giving us a range of possibilities for the estimate itself.

Let’s do an example. Say we’re interested in the effect of owning a sports car on your tendency to drive over the speed limit. We add some controls - gender, age, income, parental income, and so on. We estimate the effect and find that owning a sports car increases your chances of speeding on a given drive by 5%. There are some unmeasured things remaining, though - tendency for risk-taking, for example.

We don’t want to assume that getting a sports car is unrelated to risk-taking tendencies. That just doesn’t sound plausible. But we can say “risk-taking is likely to be positively related to both sports car ownership and speeding,” (even though we don’t know how strongly) “so risk-taking being left out of the model makes the treatment effect look more positive. If we could control for risk-taking, the treatment effect would become more negative.”

With that (much more plausible) assumption, we can’t actually say what the effect of owning a sports car on speeding is precisely, but we can say that it’s no higher than 5%. We have “bounded the effect from above” by 5%.

If we like, we can then go further. If we’re willing to make assumptions a little stronger than just the sign, we can say something like “given all the other controls, the effect of risk-taking on buying a sports car is between 0 and X.” This would let us say that the effect of sports car ownership on speeding is not just lower than 5%, but between 5% and some specific lower number, maybe 2%. We can adjust the strength of our assumptions as we like, getting more precise results with heavier assumptions, or less precise results with assumptions that don’t say as much.

Partial identification is a wide-ranging area with plenty of methods.184184 Methods that go much deeper than just figuring out the direction that an uncontrolled variable biases the estimate. Many of the details are unfortunately too technical for this book. But if you are interested, you can find a relatively gentle introduction in Gangl (⊕2013Gangl, Markus. 2013. “Partial Identification and Sensitivity Analysis.” In Handbook of Causal Analysis for Social Research, 377–402. Springer.).

Your last line of defense is your gut. After all of that - checking the reasonableness of your assumptions and what they imply, checking how precise your results can get based on how strong your assumptions are - you’re still left with a set of assumptions and a result.

And that result? Sometimes results just don’t make sense.

That’s an important thing to pay attention to. Is your result plausible at all? If it’s not, then even if you can’t figure out why or what you could do to fix it, then you have an assumption wrong somewhere. You just must.

For example, say you’re studying the effect of drinking an extra glass of water once a week on your lifespan. You carefully design your research, control for all the necessary controls, do everything you can, and you find that the extra glass of water once a week makes you live twenty years longer.

Astounding! Alert the presses.

Well, probably not. There’s just no way that’s true. Completely unbelievable. You must have made an incorrect assumption, or made an error in your statistical code, or perhaps just got a huge fluke result in your data. What you didn’t get is the real result. Not buying it.

There’s a degree of subjectivity here. We want to be willing to accept surprising results - if we weren’t, what’s the point of doing research in the first place? But many results are not just surprising but darn near impossible. And it doesn’t even need to be as extreme as a twenty-year lifespan jump. If you found that a teacher training program increased student test scores by a third of a standard deviation, is that too good to believe?185185 Even well-regarded educational interventions considered quite successful generally have effects in the range of a tenth of a standard deviation. If you found that a simple thirty-second audio message played once in a laboratory changed people’s behavior at all five years later, is that plausible? Maybe not.

So that’s the last line of defense you have. Your gut. Could this result ever possibly be? If it couldn’t, then it isn’t.